Karhunen-Loève (KL) Expansion

Karhunen-Loève (KL) Expansion#

The Karhunen-Loève (KL) Expansion is a powerful mathematical tool used to represent a zero-mean stochastic process \( n(t) \) in terms of orthogonal basis functions derived from its own autocorrelation structure.

Eigenfunction Decomposition#

The process begins by solving an eigenvalue problem involving the autocorrelation function \( R(t,\tau) \). The solutions yield a set of orthonormal eigenfunctions \( \{\Theta_i(t)\} \) and corresponding eigenvalues \( \{\lambda_i\} \).

Consider a zero-mean stochastic process \( n(t) \) with autocorrelation function \( R(t,\tau) \). Let \( \{\Theta_i(t)\}_{i=1}^\infty \) be a complete set of orthonormal functions that satisfy the eigenvalue problem:

\[ \boxed{ \int R(t,\tau) \Theta_i(\tau) \, d\tau = \lambda_i \Theta_i(t), \quad i = 1, 2, \dots } \]

Series Representation: KL Expansion of \( n(t) \)#

The stochastic process \( n(t) \) is expressed as an infinite series of these eigenfunctions, each scaled by a random coefficient \( n_i \).

This series effectively decomposes the process into uncorrelated components.

\[ n(t) = \sum_{i=1}^\infty n_i \Theta_i(t) \]

where the coefficients \( n_i \) are given by:

\[ n_i = \int n(t) \Theta_i^*(t) \, dt, \quad i = 1, 2, \dots \]

Properties of the Coefficients: Uncorrelated Coefficients#

The coefficients \( n_i \) have zero mean and are uncorrelated, as indicated by \( \mathbb{E}[n_i n_j^*] = \lambda_i \delta_{ij} \). This property simplifies the analysis and processing of the stochastic process, as each component can be treated independently.

The coefficients \( \{n_i\} \) are uncorrelated random variables with:

\[\begin{split} \begin{align*} \mathbb{E}[n_i] &= 0 \\ \mathbb{E}[n_i n_j^*] &= \lambda_i \delta_{ij} \end{align*} \end{split}\]

The Karhunen-Loève Expansion offers a structured and efficient way to analyze and represent stochastic processes by leveraging their inherent correlation properties through orthogonal function decomposition.

The KL expansion is optimal in the sense that it provides the best possible mean-square approximation of the stochastic process with a finite number of terms. This makes it highly useful in applications like signal processing, data compression, and statistical analysis.

Mercer’s Theorem#

Mercer’s Theorem underpins the KL expansion by ensuring that the autocorrelation function \( R(t,\tau) \) can be expressed as a convergent series of the eigenfunctions and eigenvalues.

The autocorrelation function can be expanded as:

\[ \boxed{ R(t,\tau) = \sum_{j=1}^\infty \lambda_j \Theta_j(t) \Theta_j^*(\tau) } \]

This guarantees that the KL expansion faithfully represents the statistical properties of the original process.

Example: KL Expansion of a White Noise Process#

In this example, the Karhunen-Loève expansion is applied to a zero-mean white noise process \( X(t) \) with a power spectral density of \( \frac{N_0}{2} \), defined over an arbitrary interval \([a, b]\).

KL Exapansion Derivation Steps:#

  1. Eigenvalue Equation: To derive the KL expansion, we first need to solve the following integral equation involving the autocorrelation function:

    \[ \int_a^b \frac{N_0}{2} \delta(t_1 - t_2) \phi_n(t_2) dt_2 = \lambda_n \phi_n(t_1), \quad a < t_1 < b \]

    Here, \( \delta(t_1 - t_2) \) is the Dirac delta function, representing the autocorrelation of the white noise process.

  2. Simplification using the Sifting Property: The sifting property of the Dirac delta function allows us to simplify the integral equation as follows:

    \[ \frac{N_0}{2} \phi_n(t_1) = \lambda_n \phi_n(t_1), \quad a < t_1 < b \]

    This equation suggests that the eigenfunctions \( \phi_n(t) \) can be any arbitrary orthonormal functions because the eigenvalue \( \lambda_n = \frac{N_0}{2} \) is constant for all \( n \).

The result indicates that any orthonormal basis can be used for the expansion of a white noise process, and all the coefficients \( X_n \) in the KL expansion will have the same variance of \( \frac{N_0}{2} \).

Thus, for white noise processes, the KL expansion allows flexibility in choosing the orthonormal functions \( \phi_n(t) \).

The coefficients resulting from the expansion will always have the same variance, given by the power spectral density \( \frac{N_0}{2} \).

import numpy as np
import matplotlib.pyplot as plt

# Parameters
N = 100  # Number of time steps
T = 1.0  # Interval length
dt = T / N  # Time step size
sigma = 1.0  # Noise intensity

# Step 1: Generate a White Noise Process
# In discrete time, white noise is i.i.d. Gaussian with variance scaled by 1/dt
np.random.seed(42)  # For reproducibility
W = np.random.normal(0, sigma / np.sqrt(dt), N)
time = np.linspace(0, T, N, endpoint=False)

# Step 2: Construct an Orthonormal Basis
# Use a Fourier basis (cosines and sines) over [0, T]
basis = np.zeros((N, N))
# Constant term
basis[0, :] = np.sqrt(1 / N)
# Cosine terms
for k in range(1, N//2 + 1):
    basis[k, :] = np.sqrt(2 / N) * np.cos(2 * np.pi * k * np.arange(N) / N)
# Sine terms
for k in range(1, N//2):
    basis[N//2 + k, :] = np.sqrt(2 / N) * np.sin(2 * np.pi * k * np.arange(N) / N)

# Verify orthonormality (optional check)
for i in range(5):
    for j in range(5):
        dot_product = np.sum(basis[i, :] * basis[j, :])
        # print(f"Dot product <phi_{i}, phi_{j}> = {dot_product:.2f}", end=" ")
    print()

# Step 3 & 4: Expand the White Noise Process and Compute Coordinates
# Coefficients Z_k = <W, phi_k>
Z = np.zeros(N)
for k in range(N):
    Z[k] = np.sum(W * basis[k, :])  # Discrete inner product

# Reconstruct the signal
W_reconstructed = np.zeros(N)
for n in range(N):
    W_reconstructed[n] = np.sum(Z * basis[:, n])

# Results
print("\nFirst 5 coefficients Z_k:", Z[:5])
print("Original W[n] (first 5):", W[:5])
print("Reconstructed W[n] (first 5):", W_reconstructed[:5])

# Visualization
plt.figure(figsize=(12, 8))

# Plot original white noise
plt.subplot(3, 1, 1)
plt.plot(time, W, label="Original White Noise W[n]")
plt.xlabel("Time")
plt.ylabel("Amplitude")
plt.title("White Noise Process")
plt.legend()

# Plot first few basis functions
plt.subplot(3, 1, 2)
for k in range(3):
    plt.plot(time, basis[k, :], label=f"phi_{k}(t)")
plt.xlabel("Time")
plt.ylabel("Amplitude")
plt.title("First 3 Basis Functions")
plt.legend()

# Plot original vs reconstructed
plt.subplot(3, 1, 3)
plt.plot(time, W, label="Original W[n]", alpha=0.7)
plt.plot(time, W_reconstructed, '--', label="Reconstructed W[n]", alpha=0.7)
plt.xlabel("Time")
plt.ylabel("Amplitude")
plt.title("Original vs Reconstructed White Noise")
plt.legend()

plt.tight_layout()
plt.show()

# Compute mean squared error to verify reconstruction
mse = np.mean((W - W_reconstructed)**2)
print(f"Mean Squared Error between original and reconstructed: {mse:.2e}")

First 5 coefficients Z_k: [-10.38465174   2.301302     6.58712585  13.29551733   6.81870197]
Original W[n] (first 5): [ 4.96714153 -1.38264301  6.47688538 15.23029856 -2.34153375]
Reconstructed W[n] (first 5): [ 4.64885039 -1.06435188  6.15859424 15.5485897  -2.65982488]
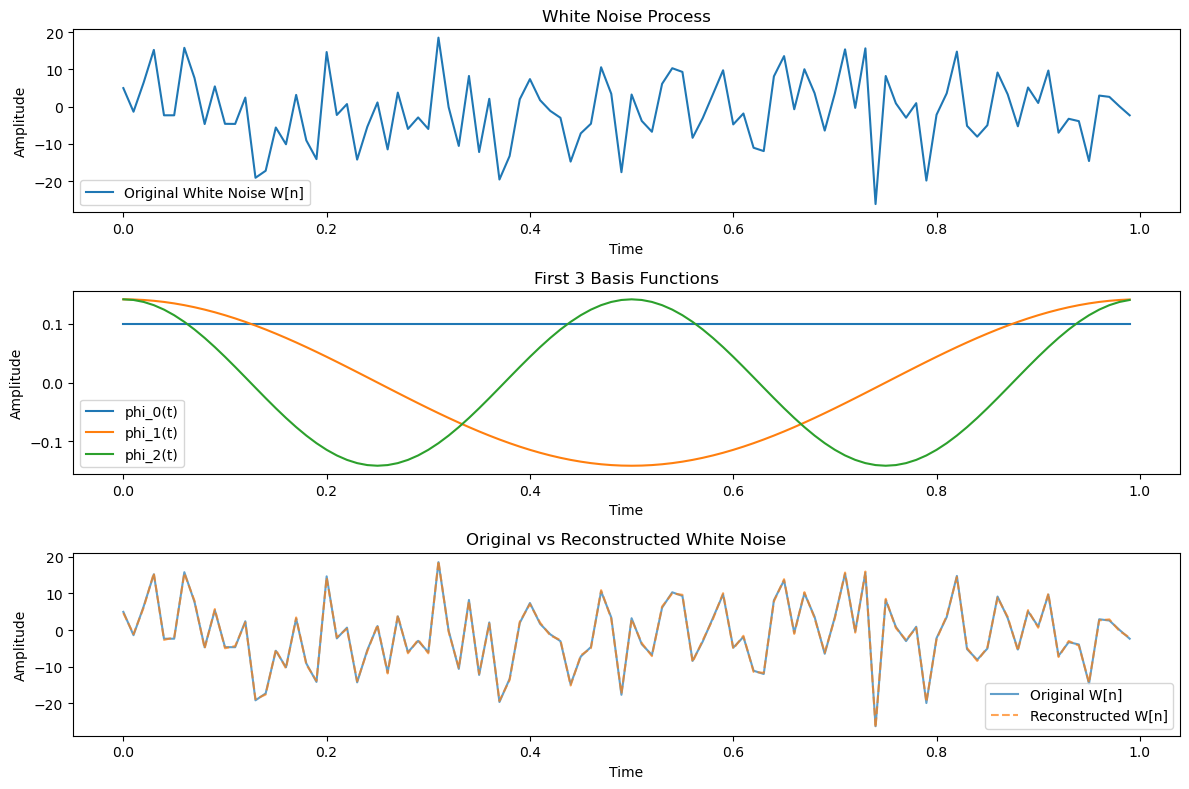
_images/f04000b312fe23ee16f4da92e5bdf10203eede6766376623ca53c15a5aa1789a.png 
Mean Squared Error between original and reconstructed: 1.01e-01