Set Theory

Set Theory

Before diving into probability theory, it is essential to review set theory, as it forms the foundation upon which probabilistic models are built.

Understanding the concepts of sets, subsets, unions, intersections, and complements is crucial for tackling complex probabilistic scenarios, particularly when calculating the probability of various combinations of outcomes.

Definitions

Set
A set is a collection of objects or elements.

Elements of a Set
The objects that make up a set are referred to as its elements.

• If \( x \) is an element of a set \( \mathbb{A} \), it is written as \( x \in \mathbb{A} \).

• If \( y \) is not an element of \( \mathbb{A} \), it is written as \( y \notin \mathbb{A} \).

Experiment
An experiment is a procedure—often hypothetical—that is performed to produce some result.

Outcome
An outcome is a possible result of an experiment.

Examples

Based on the given definitions, considering the example of rolling a die:

• For rolling a die, the set is \( \{1, 2, 3, 4, 5, 6\} \), often referred to as the sample space.

• For example, \( 1 \), \( 2 \), \( 3 \), \( 4 \), \( 5 \), and \( 6 \) are the elements of the set \( \{1, 2, 3, 4, 5, 6\} \).

• In this case, the experiment is rolling a die.

• For example, rolling a \( 3 \) or a \( 5 \) is a possible outcome of rolling the die.

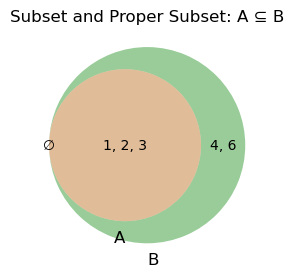
Subset

A set \( \mathbb{A} \) is called a subset of another set \( \mathbb{B} \) if all elements of \( \mathbb{A} \) are also in \( \mathbb{B} \). This is written as:

\[ \mathbb{A} \subseteq \mathbb{B} \]

• Equal Sets: If \( \mathbb{A} \subseteq \mathbb{B} \) and \( \mathbb{B} \subseteq \mathbb{A} \), then the two sets are equal, meaning they have exactly the same elements.

• Proper Subset: If \( \mathbb{A} \subseteq \mathbb{B} \) but there are elements in \( \mathbb{B} \) that are not in \( \mathbb{A} \), then \( \mathbb{A} \) is a proper subset of \( \mathbb{B} \), written as:

  \[ \mathbb{A} \subset \mathbb{B} \]

Universal Set and Empty Set

• Universal Set: The universal set, \( \mathbb{S} \), is the set of all objects being considered in a particular problem.

• Empty Set: The empty set, \( \varnothing \), is the set that contains no elements.

These concepts are key building blocks in set theory and are widely used in probability, where subsets represent events, and the universal set represents the sample space.

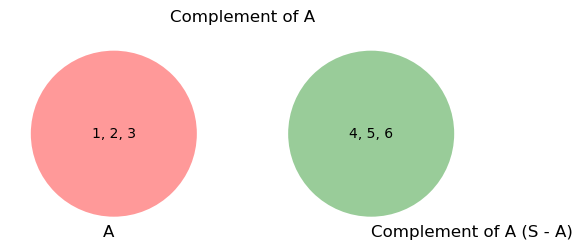
Complement Set

The complement of a set \( \mathbb{A}, \) written as \( \bar{\mathbb{A}} \), or \( \mathbb{A}^{c} \), is the set of all elements in the universal set \( \mathbb{S} \) that are not in \( \mathbb{A} \).

Simulation

import matplotlib.pyplot as plt
from matplotlib_venn import venn2

# Define sets
universal_set = {1, 2, 3, 4, 5, 6}
A = {1, 2, 3}
B = {1, 2, 3, 4, 6}
C = {2, 3, 5}
complement_A = universal_set - A
difference_set = B - A
empty_set = set()

# Function to safely label Venn diagram elements
def label_venn_elements(venn, subset_labels):
    for label_id, elements in subset_labels.items():
        label = venn.get_label_by_id(label_id)
        if label:  # Check if the subset exists in the diagram
            label.set_text(', '.join(map(str, elements)) if elements else '∅')

# Venn diagram for subset and proper subset
plt.figure(figsize=(6, 3))
venn = venn2(subsets=(len(A - B), len(B - A), len(A & B)), set_labels=("A", "B"))
label_venn_elements(venn, {'10': A - B, '01': B - A, '11': A & B})
plt.title("Subset and Proper Subset: A ⊆ B")
plt.show()

# Venn diagram for universal set and empty set
plt.figure(figsize=(6, 3))
venn = venn2(subsets=(len(universal_set), 0, 0), set_labels=("Universal Set (S)", "Empty Set (∅)"))
label_venn_elements(venn, {'10': universal_set, '01': empty_set, '11': empty_set})
plt.title("Universal Set and Empty Set")
plt.show()

# Venn diagram for complement of A
plt.figure(figsize=(6, 3))
venn = venn2(subsets=(len(A), len(complement_A), 0), set_labels=("A", "Complement of A (S - A)"))
label_venn_elements(venn, {'10': A, '01': complement_A, '11': empty_set})
plt.title("Complement of A")
plt.show()

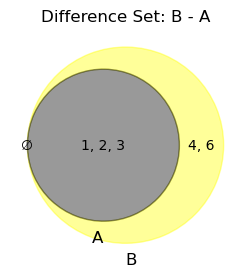
Difference Set

For two sets \( \mathbb{A} \) and \( \mathbb{B} \) where \( \mathbb{A} \subseteq \mathbb{B} \), the difference set, written \( \mathbb{B} - \mathbb{A} \), consists of elements in \( \mathbb{B} \) that are not in \( \mathbb{A} \).

Key Properties of Sets

• For any set \( \mathbb{A} \):

  \[ \varnothing \subseteq \mathbb{A} \subseteq \mathbb{S}, \quad \mathbb{A} \subseteq \mathbb{A} \]

• If \( \mathbb{A} \subseteq \mathbb{B} \) and \( \mathbb{B} \subseteq \mathbb{C} \), then \( \mathbb{A} \subseteq \mathbb{C} \).

• The complement of the universal set is the empty set:

  \[ \bar{\mathbb{S}} = \varnothing \]

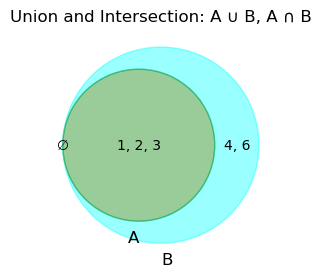
Union and Intersection

• The union of two sets \( \mathbb{A} \) and \( \mathbb{B} \), written \( \mathbb{A} \cup \mathbb{B} \), includes all elements in \( \mathbb{A} \), \( \mathbb{B} \), or both.

• The intersection of two sets \( \mathbb{A} \) and \( \mathbb{B} \), written \( \mathbb{A} \cap \mathbb{B} \), includes only the elements common to both sets.

For an element \( x \):

\[ \mathbb{A} \cup \mathbb{B} = \{x \mid x \in \mathbb{A} \text{ OR } x \in \mathbb{B}\}, \quad \mathbb{A} \cap \mathbb{B} = \{x \mid x \in \mathbb{A} \text{ AND } x \in \mathbb{B}\} \]

Here, the symbol \( \mid \) means “such that.”

These operations form the basis of many concepts in probability and logic, helping to define events and their relationships.

# Venn diagram for difference set: B - A
plt.figure(figsize=(6, 3))
venn = venn2(subsets=(len(A - B), len(B - A), len(A & B)), set_labels=("A", "B"))
label_venn_elements(venn, {'10': A - B, '01': B - A, '11': A & B})
# Highlight only the difference B - A
venn.get_patch_by_id('01').set_color('yellow')  # Shade only B - A
venn.get_patch_by_id('10').set_color((0, 0, 0, 0))  # Make A - B transparent
venn.get_patch_by_id('11').set_color((0, 0, 0, 0))  # Make A ∩ B transparent
plt.title("Difference Set: B - A")
plt.show()

# Venn diagram for union and intersection
plt.figure(figsize=(6, 3))
venn = venn2(subsets=(len(A - B), len(B - A), len(A & B)), set_labels=("A", "B"))
label_venn_elements(venn, {'10': A - B, '01': B - A, '11': A & B})
# Highlight the union and intersection
venn.get_patch_by_id('10').set_color('cyan')  # Shade A - B
venn.get_patch_by_id('01').set_color('cyan')  # Shade B - A
venn.get_patch_by_id('11').set_color('green')  # Shade A ∩ B
plt.title("Union and Intersection: A ∪ B, A ∩ B")
plt.show()

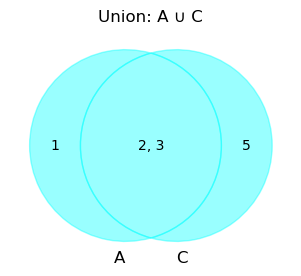
# Venn diagram for union between A and C
plt.figure(figsize=(6, 3))
venn = venn2(subsets=(len(A - C), len(C - A), len(A & C)), set_labels=("A", "C"))
label_venn_elements(venn, {'10': A - C, '01': C - A, '11': A & C})
# Highlight the union with transparency
venn.get_patch_by_id('10').set_color((0, 1, 1, 0.5))  # Cyan with transparency
venn.get_patch_by_id('01').set_color((0, 1, 1, 0.5))  # Cyan with transparency
venn.get_patch_by_id('11').set_color((0, 1, 1, 0.7))  # Cyan, slightly opaque for overlap
plt.title("Union: A ∪ C")
plt.show()

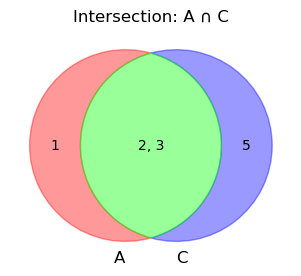
# Venn diagram for intersection between A and C
plt.figure(figsize=(6, 3))
venn = venn2(subsets=(len(A - C), len(C - A), len(A & C)), set_labels=("A", "C"))
label_venn_elements(venn, {'10': A - C, '01': C - A, '11': A & C})
# Highlight the intersection with a different color
venn.get_patch_by_id('10').set_color((1, 0, 0, 0.3))  # Red with transparency for A - C
venn.get_patch_by_id('01').set_color((0, 0, 1, 0.3))  # Blue with transparency for C - A
venn.get_patch_by_id('11').set_color((0, 1, 0, 0.7))  # Green, slightly opaque for overlap
plt.title("Intersection: A ∩ C")
plt.show()

Mutually Exclusive Sets

Two sets \( \mathbb{A} \) and \( \mathbb{B} \) are mutually exclusive or disjoint if they have no elements in common. This is expressed as:

\[ \mathbb{A} \cap \mathbb{B} = \varnothing \]

A collection of sets \( \mathbb{A}_1, \mathbb{A}_2, \ldots, \mathbb{A}_n \) is said to be exhaustive if every element in the universal set \( \mathbb{S} \) belongs to at least one of these sets. For exhaustive sets:

\[ \mathbb{A}_1 \cup \mathbb{A}_2 \cup \ldots \cup \mathbb{A}_n = \mathbb{S} \]

Boolean Operations on Sets

• Boolean Algebra: A field of mathematics that focuses on operations involving logical values represented by binary variables (0 or 1).

• Boolean Operations on Sets: These operations apply the principles of Boolean algebra to sets, defining relationships like union, intersection, and complement based on logical rules.

Additional Resources:

• Logical (Boolean) Operations in MATLAB

• Logic Functions with NumPy

The Algebra of Sets

The following laws are derived from the basic definitions and operations of set theory:

• Idempotent Laws:
  \( \mathbb{A} \cup \mathbb{A} = \mathbb{A} \)
  \( \mathbb{A} \cap \mathbb{A} = \mathbb{A} \)
  These hold for all sets \( \mathbb{A} \).

• Commutative Laws:
  \( \mathbb{A} \cup \mathbb{B} = \mathbb{B} \cup \mathbb{A} \)
  \( \mathbb{A} \cap \mathbb{B} = \mathbb{B} \cap \mathbb{A} \)
  These hold for all sets \( \mathbb{A} \) and \( \mathbb{B} \).

• Associative Laws:
  \( \mathbb{A} \cup (\mathbb{B} \cup \mathbb{C}) = (\mathbb{A} \cup \mathbb{B}) \cup \mathbb{C} = \mathbb{A} \cup \mathbb{B} \cup \mathbb{C} \)
  \( \mathbb{A} \cap (\mathbb{B} \cap \mathbb{C}) = (\mathbb{A} \cap \mathbb{B}) \cap \mathbb{C} = \mathbb{A} \cap \mathbb{B} \cap \mathbb{C} \)
  These hold for all sets \( \mathbb{A} \), \( \mathbb{B} \), and \( \mathbb{C} \).

• Distributive Laws:
  \( \mathbb{A} \cap (\mathbb{B} \cup \mathbb{C}) = (\mathbb{A} \cap \mathbb{B}) \cup (\mathbb{A} \cap \mathbb{C}) \)
  \( \mathbb{A} \cup (\mathbb{B} \cap \mathbb{C}) = (\mathbb{A} \cup \mathbb{B}) \cap (\mathbb{A} \cup \mathbb{C}) \)
  These hold for all sets \( \mathbb{A} \), \( \mathbb{B} \), and \( \mathbb{C} \).

• Consistency (Mutual Equivalence):
  The conditions below are consistent or equivalent:

  1. \( \mathbb{A} \subseteq \mathbb{B} \)

  2. \( \mathbb{A} \cap \mathbb{B} = \mathbb{A} \)

  3. \( \mathbb{A} \cup \mathbb{B} = \mathbb{B} \)

These laws are foundational for reasoning about sets and form the basis for further exploration in probability and logic.

• Universal Bounds:
  \( \varnothing \subseteq \mathbb{A} \subseteq \mathbb{S} \) for all sets \( \mathbb{A} \).

• Product:
  \( \varnothing \cap \mathbb{A} = \varnothing \)
  \( \mathbb{S} \cap \mathbb{A} = \mathbb{A} \)
  These hold for all sets \( \mathbb{A} \).

• Sum:
  \( \varnothing \cup \mathbb{A} = \mathbb{A} \)
  \( \mathbb{S} \cup \mathbb{A} = \mathbb{S} \)
  These hold for all sets \( \mathbb{A} \).

• Involution:
  \( \overline{\overline{\mathbb{A}}} = \mathbb{A} \)
  This holds for all sets \( \mathbb{A} \).

• Complementarity:
  \( \mathbb{A} \cup \overline{\mathbb{A}} = \mathbb{S} \)
  \( \mathbb{A} \cap \overline{\mathbb{A}} = \varnothing \)
  These hold for all sets \( \mathbb{A} \).

• DeMorgan’s First Law:
  \( \overline{\mathbb{A} \cup \mathbb{B}} = \overline{\mathbb{A}} \cap \overline{\mathbb{B}} \)
  This holds for all sets \( \mathbb{A} \) and \( \mathbb{B} \).

• DeMorgan’s Second Law:
  \( \overline{\mathbb{A} \cap \mathbb{B}} = \overline{\mathbb{A}} \cup \overline{\mathbb{B}} \)
  This holds for all sets \( \mathbb{A} \) and \( \mathbb{B} \).

Mathematical Proofs for DeMorgan’s Laws

DeMorgan’s First Law:

\[ \overline{\mathbb{A} \cup \mathbb{B}} = \overline{\mathbb{A}} \cap \overline{\mathbb{B}} \]

Proof:

For the Left-Hand-Side (LHS), by definition, the complement of a union:

\[ \overline{\mathbb{A} \cup \mathbb{B}} = \{x \in \mathbb{S} \mid x \notin (\mathbb{A} \cup \mathbb{B})\} \]

Using the definition of union:

\[ \mathbb{A} \cup \mathbb{B} = \{x \in \mathbb{S} \mid x \in \mathbb{A} \text{ or } x \in \mathbb{B}\} \]

Hence:

\[ \overline{\mathbb{A} \cup \mathbb{B}} = \{x \in \mathbb{S} \mid x \notin \mathbb{A} \text{ and } x \notin \mathbb{B}\} \]

For the Right-Hand-Side (RHS), by the definition of intersection and complements:

\[ \overline{\mathbb{A}} \cap \overline{\mathbb{B}} = \{x \in \mathbb{S} \mid x \notin \mathbb{A}\} \cap \{x \in \mathbb{S} \mid x \notin \mathbb{B}\} \]

which simplifies to:

\[ \overline{\mathbb{A}} \cap \overline{\mathbb{B}} = \{x \in \mathbb{S} \mid x \notin \mathbb{A} \text{ and } x \notin \mathbb{B}\} \]

Combining above steps, we have

\[ \overline{\mathbb{A} \cup \mathbb{B}} = \overline{\mathbb{A}} \cap \overline{\mathbb{B}} \]

Consider the specific sets \( A = \{1, 2, 3\} \) and \( B = \{1, 2, 3, 4, 6\} \), we have:

Using the Given Sets:

• Universal Set: \( \mathbb{S} = \{1, 2, 3, 4, 5, 6\} \)

• Set A: \( \mathbb{A} = \{1, 2, 3\} \)

• Set B: \( \mathbb{B} = \{1, 2, 3, 4, 6\} \)

For the LHS, calculate \( \mathbb{A} \cup \mathbb{B} \):

\[ \mathbb{A} \cup \mathbb{B} = \{1, 2, 3, 4, 6\} \]

Calculate \( \overline{\mathbb{A} \cup \mathbb{B}} \):

\[ \overline{\mathbb{A} \cup \mathbb{B}} = \mathbb{S} - (\mathbb{A} \cup \mathbb{B}) = \{5\} \]

For the RHS, calculate \( \overline{\mathbb{A}} \) and \( \overline{\mathbb{B}} \):

\[ \overline{\mathbb{A}} = \mathbb{S} - \mathbb{A} = \{4, 5, 6\} \]

\[ \overline{\mathbb{B}} = \mathbb{S} - \mathbb{B} = \{5\} \]

Calculate \( \overline{\mathbb{A}} \cap \overline{\mathbb{B}} \):

\[ \overline{\mathbb{A}} \cap \overline{\mathbb{B}} = \{4, 5, 6\} \cap \{5\} = \{5\} \]

Verify Equality:

\[ \overline{\mathbb{A} \cup \mathbb{B}} = \{5\}, \quad \overline{\mathbb{A}} \cap \overline{\mathbb{B}} = \{5\} \]

Therefore:

\[ \overline{\mathbb{A} \cup \mathbb{B}} = \overline{\mathbb{A}} \cap \overline{\mathbb{B}} \]

\(\blacksquare\)

complement_A = universal_set - A
complement_B = universal_set - B

# DeMorgan's First Law: \overline{A \cup B} = \overline{A} \cap \overline{B}
plt.figure(figsize=(6, 3))
left_side = universal_set - (A | B)  # \overline{A \cup B}
right_side = (complement_A & complement_B)  # \overline{A} \cap \overline{B}
venn = venn2(subsets=(len(left_side - right_side), len(right_side - left_side), len(left_side & right_side)))
label_venn_elements(venn, {'10': left_side - right_side, '01': right_side - left_side, '11': left_side & right_side})
plt.title("DeMorgan's First Law")
plt.show()

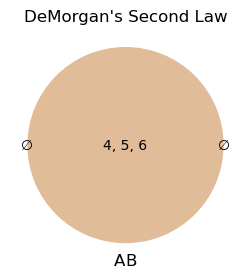
DeMorgan’s Second Law:

\[ \overline{\mathbb{A} \cap \mathbb{B}} = \overline{\mathbb{A}} \cup \overline{\mathbb{B}} \]

Proof:

For the LHS, by definition, the complement of an intersection:

\[ \overline{\mathbb{A} \cap \mathbb{B}} = \{x \in \mathbb{S} \mid x \notin (\mathbb{A} \cap \mathbb{B})\} \]

Using the definition of intersection:

\[ \mathbb{A} \cap \mathbb{B} = \{x \in \mathbb{S} \mid x \in \mathbb{A} \text{ and } x \in \mathbb{B}\} \]

Hence:

\[ \overline{\mathbb{A} \cap \mathbb{B}} = \{x \in \mathbb{S} \mid x \notin \mathbb{A} \text{ or } x \notin \mathbb{B}\} \]

For the RHS, by the definition of union and complements:

\[ \overline{\mathbb{A}} \cup \overline{\mathbb{B}} = \{x \in \mathbb{S} \mid x \notin \mathbb{A}\} \cup \{x \in \mathbb{S} \mid x \notin \mathbb{B}\} \]

which simplifies to:

\[ \overline{\mathbb{A}} \cup \overline{\mathbb{B}} = \{x \in \mathbb{S} \mid x \notin \mathbb{A} \text{ or } x \notin \mathbb{B}\} \]

Combining the above steps, we have:

\[ \overline{\mathbb{A} \cap \mathbb{B}} = \overline{\mathbb{A}} \cup \overline{\mathbb{B}} \]

Consider the specific sets \( A = \{1, 2, 3\} \) and \( B = \{1, 2, 3, 4, 6\} \), we have:

Using the Given Sets:

For the LHS, calculate \( \mathbb{A} \cap \mathbb{B} \):

\[ \mathbb{A} \cap \mathbb{B} = \{1, 2, 3\} \]

Calculate \( \overline{\mathbb{A} \cap \mathbb{B}} \):

\[ \overline{\mathbb{A} \cap \mathbb{B}} = \mathbb{S} - (\mathbb{A} \cap \mathbb{B}) = \{4, 5, 6\} \]

For the RHS, calculate \( \overline{\mathbb{A}} \) and \( \overline{\mathbb{B}} \) (already calculated above):

\[ \overline{\mathbb{A}} = \{4, 5, 6\}, \quad \overline{\mathbb{B}} = \{5\} \]

Calculate \( \overline{\mathbb{A}} \cup \overline{\mathbb{B}} \):

\[ \overline{\mathbb{A}} \cup \overline{\mathbb{B}} = \{4, 5, 6\} \cup \{5\} = \{4, 5, 6\} \]

Verify Equality:

\[ \overline{\mathbb{A} \cap \mathbb{B}} = \{4, 5, 6\}, \quad \overline{\mathbb{A}} \cup \overline{\mathbb{B}} = \{4, 5, 6\} \]

Therefore:

\[ \overline{\mathbb{A} \cap \mathbb{B}} = \overline{\mathbb{A}} \cup \overline{\mathbb{B}} \]

\(\blacksquare\)

# DeMorgan's Second Law: \overline{A \cap B} = \overline{A} \cup \overline{B}
plt.figure(figsize=(6, 3))
left_side = universal_set - (A & B)  # \overline{A \cap B}
right_side = (complement_A | complement_B)  # \overline{A} \cup \overline{B}
venn = venn2(subsets=(len(left_side - right_side), len(right_side - left_side), len(left_side & right_side)))
label_venn_elements(venn, {'10': left_side - right_side, '01': right_side - left_side, '11': left_side & right_side})
plt.title("DeMorgan's Second Law")
plt.show()