A Logarithmic Measurement of Information#
Introduction to Measuring Information#
To develop a quantitative measure of information, we consider two discrete random variables, \(X\) and \(Y\), representing outcomes from information sources.
Variable \(X\) takes values from an alphabet \(\mathcal{X}\), while \(Y\) takes values from an alphabet \(\mathcal{Y}\).
These alphabets are finite sets of possible symbols (for instance, \(\mathcal{X} = \{0, 1\}\) for a binary source or \(\mathcal{Y} = \{A, B, C\}\) for a text source).
The main question is: How much information does observing a specific outcome \(\{Y = y\}\) provide about a specific outcome \(\{X = x\}\)?
The measure of information should reflect how much uncertainty about \(X\) is reduced by knowing \(Y\), a central concept in information theory.
Amount of Information in the Context of Observation#
Suppose we observe the event \(\{Y = y\}\); we want to determine how much information this observation gives us about \(\{X = x\}\).
The answer depends on the statistical relationship between \(X\) and \(Y\).
Intuitively, if \(\{Y = y\}\) tells us something definitive about \(\{X = x\}\), it provides significant information; if it tells us nothing, the information gained is zero.
This perspective—information as reduction in uncertainty—underpins many communication models in which one variable (e.g., the transmitted signal) helps us infer another (e.g., the received signal).
Case of Statistical Independence#
If \(X\) and \(Y\) are statistically independent, i.e.:
observing \(\{Y = y\}\) provides no information about \(\{X = x\}\).
In such a scenario, knowing \(\{Y = y\}\) does not alter the probability distribution of \(X\).
For example, if \(X\) represents a coin toss and \(Y\) a die roll, then observing \(Y = 4\) has no bearing on whether \(X = \text{heads}\). Hence, there is no reduction in uncertainty about \(X\).
Case of Full Dependence#
At the other extreme, if \(X\) and \(Y\) are fully dependent, observing \(\{Y = y\}\) uniquely determines \(\{X = x\}\).
In this case, there is a one-to-one correspondence: for each \(y \in \mathcal{Y}\), there is exactly one \(x \in \mathcal{X}\) such that \(\Pr(X = x \mid Y = y) = 1\).
Here, knowing \(\{Y = y\}\) eliminates all uncertainty about \(X\); the information gained from \(\{Y = y\}\) is therefore equivalent to the entire information of the event \(\{X = x\}\).
An example is when \(Y\) is a perfect copy of \(X\): once \(Y\) is observed, \(X\) is known with certainty.
Information Content (Self-Information)#
Definition of Self-Information#
The information content—also referred to as self-information, surprisal, or Shannon information—quantifies how much information is gained upon observing a particular event.
For a discrete random variable \(X\) that takes a value \(x_k\) with probability \(P[x_k]\), the self-information \(I(x_k)\) is defined as:
where \(b\) is the base of the logarithm.
This logarithmic definition captures the surprise associated with an outcome: rare events (small \(P[x_k]\)) correspond to larger self-information, while certain events (large \(P[x_k]\)) correspond to lower self-information. The negative sign ensures \(I(x_k)\) is nonnegative, matching the intuition that information should be a positive quantity.
Units of Information#
The base \(b\) of the logarithm determines the unit in which self-information is measured:
Base \(b = 2\): The unit is bits (binary digits). This is the most common choice in digital communications because it aligns directly with binary systems. One bit represents the information gained by distinguishing between two equally likely outcomes.
Base \(b = e\): The unit is nats, where the natural logarithm is used. This is often preferred in theoretical settings due to its convenience in calculus-based derivations.
Base \(b = 10\): The unit is hartleys (or bans).
For example, if \(P[x_k] = 0.5\) and \(b = 2\), e.g., equiprobable BPSK, then
which corresponds to the information obtained from a fair coin toss (i.e., one bit of surprise).
Properties of Self-Information#
Zero Information for Certain Events#
A fundamental property of self-information is that it equals zero for events that occur with certainty:
Because \(\log_b(1) = 0\) for any logarithmic base \(b\), the term \(-\log_b\bigl(P[x_k]\bigr)\) becomes zero when \(P[x_k] = 1\).
In practical terms, if we know an event will occur (e.g., a biased coin that always lands heads), observing that event provides no new information.
Non-Negative Information#
Self-information is always non-negative:
Since \(P[x_k]\) is at most \(1\), its reciprocal \(1 / P[x_k]\) is at least 1, making \(\log_b\bigl(1 / P[x_k]\bigr)\) non-negative.
The negative sign in the definition \(\,I(x_k) = -\log_b\bigl(P[x_k]\bigr)\) ensures \(I(x_k)\) remains greater than or equal to zero.
This aligns with the idea that observing an event cannot increase uncertainty; it can only reduce it (or do nothing).
More Information for Less Probable Events#
Self-information grows larger as an event becomes less probable:
Because \(\log_b\) is a monotonically increasing function, a smaller probability \(P[x_k]\) yields a larger value \(-\log_b\bigl(P[x_k]\bigr)\).
For example, if \(P[x_k] = 0.25\) and \(P[x_i] = 0.5\) (with \(b = 2\)), then
This demonstrates that rarer events carry greater information when they occur.
Additivity for Independent Events#
For independent events, the total self-information is the sum of the individual self-informations.
If events \(x_k\) and \(x_l\) are statistically independent, then
and thus
This additivity confirms that the information gained from observing two independent events is simply the sum of the information gained from each event separately.
Rationale and Example of Logarithmic Measure#
The logarithmic definition of self-information,
is motivated by two primary considerations:
Additivity for Independent Events
As shown earlier, if two events are statistically independent, the self-information of their joint occurrence is the sum of their individual self-informations.The logarithm naturally provides this additive property because \(\log_b(p_1 p_2) = \log_b(p_1) + \log_b(p_2)\).
Inversely Proportional to Probability
Logarithms invert the probability in a way that aligns with intuition: the less likely an event is, the more information it conveys when it occurs.Thus, as \(P[x_k]\) decreases, \(I(x_k)\) increases.
These properties make the logarithmic measure both robust and practical, reflecting our intuitive sense of information as a reduction in uncertainty.
Example: Fair Coin Toss#
Consider a fair coin that can land heads or tails with equal probability \(\tfrac{1}{2}\). Using base-2 logarithms, the self-information for each outcome is:
Hence, each outcome provides 1 bit of information.
Initially, there are two equally likely possibilities, representing maximum uncertainty (1 bit). Observing the actual result (head or tail) resolves this uncertainty entirely, which we quantify as 1 bit of information.
Interpretation of One Bit
This example highlights a fundamental principle: one bit of information is the amount gained when one of two equally likely (equiprobable) events is observed.
The term “bit” (binary digit) encapsulates this concept in the context of digital systems, where a single binary value (0 or 1) is sufficient to encode one of two equally likely outcomes.
Mutual Information#
Definition of Mutual Information#
To quantify the information that one event provides about another, we introduce mutual information, a measure of statistical dependence between two random variables.
Consider two discrete random variables, \(X\) and \(Y\), with possible outcomes in the alphabets \(\mathcal{X}\) and \(\mathcal{Y}\), respectively.
We aim to determine how much the occurrence of an event \(\{Y = y\}\) reveals about the event \(\{X = x\}\).
A natural way to measure this is by comparing the conditional probability \(P[X = x \mid Y = y]\) (which accounts for knowledge of \(\{Y = y\}\)) to the unconditional probability \(P[X = x]\) (which assumes no knowledge of \(Y\)).
These probabilities are written as:
The mutual information between the specific outcomes \(x\) and \(y\) is defined as:
This measure quantifies how much the observation of \(\{Y = y\}\) reduces the uncertainty about \(\{X = x\}\).
If \(X\) and \(Y\) are independent, then \(P[x \mid y] = P[x]\), so the ratio equals 1, and:
\[ I(x; y) = \log_b 1 = 0. \]This means \(\{Y = y\}\) provides no information about \(\{X = x\}\), consistent with statistical independence.
If \(P[x \mid y]\) is significantly different from \(P[x]\), then \(I(x; y)\) increases, indicating a stronger dependency.
Intuitive Interpretation
The ratio:
compares the likelihood of \(\{X = x\}\) given \(\{Y = y\}\) to its prior likelihood.
If the ratio is greater than 1, then knowing \(\{Y = y\}\) makes \(\{X = x\}\) more likely, meaning that \(\{Y = y\}\) adds information about \(X\).
If the ratio is less than 1, then knowing \(\{Y = y\}\) makes \(\{X = x\}\) less likely, which still provides information by reducing uncertainty in a different way.
The logarithm transforms this ratio into an additive measure, ensuring consistency with other information-theoretic concepts like self-information and entropy.
Notation Note: In the following sections, for simplicity, \(\log_b(\cdot)\) is written as \(\log(\cdot)\), indicating that the expressions hold for any base.
Average Mutual Information#
Definition of Mutual Information Between Random Variables#
While \(I(x; y)\) measures the information shared between specific outcomes, communication systems typically analyze information at the level of entire random variables.
The mutual information between two discrete random variables \(X\) and \(Y\), denoted as \(I(X; Y)\), is the expected value of \(I(x; y)\) over all possible pairs \((x, y)\). It is defined as:
substituting \(I(x; y)\):
Here, \(P[X = x, Y = y]\) is the joint probability of observing the pair \((x, y)\), and the double summation accounts for all possible values of \(x \in \mathcal{X}\) and \(y \in \mathcal{Y}\).
This expectation represents the average reduction in uncertainty about \(X\) given knowledge of \(Y\), making it a fundamental concept in information theory for quantifying statistical dependencies.
Alternative Expression#
Using the relationship:
we can rewrite mutual information as:
Since \(P[x \mid y] P[Y = y] = P[X = x, Y = y]\), this formulation highlights that \(I(X; Y)\) measures how much the joint distribution \(P(X, Y)\) deviates from the product of the marginal distributions \(P(X) P(Y)\).
This deviation quantifies the statistical dependence between \(X\) and \(Y\).
If \(X\) and \(Y\) are independent, then \(P[X = x, Y = y] = P[x] P[y]\), leading to:
\[ I(X; Y) = \sum_{x} \sum_{y} P[x] P[y] \log \frac{P[x] P[y]}{P[x] P[y]} = \sum_{x} \sum_{y} P[x] P[y] \log 1 = 0. \]This confirms that independent variables share no mutual information.
If \(X\) and \(Y\) are dependent, the ratio \(\frac{P[X = x, Y = y]}{P[x] P[Y = y]}\) deviates from 1, and \(I(X; Y)\) increases accordingly.
Units of Mutual Information#
The units of \(I(X; Y)\) depend on the logarithm’s base:
Base 2: The unit is bits, commonly used in digital communication.
If \(I(X; Y) = 1\) bit, then observing \(Y\) reduces uncertainty about \(X\) by the equivalent of a single binary decision.
Base \(e\) (natural logarithm): The unit is nats, often preferred in mathematical and theoretical contexts due to its convenience in analytical derivations, e.g., in optimization problems.
The conversion between units follows from the logarithm change-of-base formula:
Thus, mutual information measured in nats is approximately 0.69315 times the value in bits. For instance, if:
This conversion is useful when switching between different bases for computation and analysis.
Properties of Mutual Information#
Symmetry#
Mutual information satisfies the symmetry property:
This arises from the definition:
Using the identity:
it follows that \(I(Y; X) = I(X; Y)\). This means that the information that \(Y\) provides about \(X\) is exactly the same as the information that \(X\) provides about \(Y\), reflecting the mutual nature of statistical dependence.
Non-Negativity#
Mutual information is always non-negative:
with equality if and only if \(X\) and \(Y\) are independent.
This follows from the fact that mutual information can be expressed as the Kullback-Leibler (KL) divergence between the joint distribution \(P(X, Y)\) and the product of the marginal distributions \(P(X) P(Y)\):
Since KL divergence is always non-negative, it follows that \(I(X; Y) \geq 0\).
If \(X\) and \(Y\) are independent, then \(P[x \mid y] = P[x]\), making the ratio inside the logarithm equal to 1:
\[ \log \frac{P[x \mid y]}{P[x]} = \log 1 = 0. \]This leads to \(I(X; Y) = 0\), meaning no mutual information.
If \(X\) and \(Y\) are dependent, the conditional probabilities differ from the marginals, making the logarithm positive and contributing to \(I(X; Y) > 0\).
Discussion. Unlike mutual information \(I(X; Y)\), which is always non‑negative, pointwise mutual information (PMI) for specific outcomes, defined as
can be positive, negative, or zero.
The sign of \(I(x; y)\) depends entirely on the ratio
equivalently \(\frac{P[x\mid y]}{P[x]}\). Because the logarithm is:
Positive when its argument \(>1\)
Zero when its argument \(=1\)
Negative when its argument \(<1\)
PMI can therefore take any real value (\(-\infty<I(x;y)<+\infty\)).
Contrast with Mutual Information
Mutual information \(I(X;Y)\) is the expected value of PMI over all \((x,y)\):
Because it equals a Kullback–Leibler divergence (which is always non‑negative), \(I(X;Y)\ge0\).
However, this non‑negativity does not apply to the individual PMI terms \(I(x;y)\), which may be negative, zero, or positive depending on the data.
Upper Bound#
Mutual information has an upper bound:
where \(H(X)\) and \(H(Y)\) are the entropies of \(X\) and \(Y\):
Since entropy represents the total uncertainty in a variable, mutual information—which quantifies the reduction in uncertainty—cannot exceed the lower of the two entropies.
For a uniform distribution over an alphabet of size \(k\), the maximum entropy is:
Thus, an alternative bound is:
where \(|\mathcal{X}|\) and \(|\mathcal{Y}|\) are the sizes (cardinalities) of the alphabets \(\mathcal{X}\) and \(\mathcal{Y}\).
For example, if \(|\mathcal{X}| = 2\) and \(|\mathcal{Y}| = 4\), then:
Entropy#
Mutual Information Under Independence#
When two random variables \(X\) and \(Y\) are statistically independent, the conditional probability simplifies to
meaning that knowing \(\{Y = y\}\) provides no information about \(\{X = x\}\).
Substituting this into the mutual information formula:
Notation Notes
\(I(x;y)\) is referred to as the pointwise mutual information (PMI), which can be denoted as \(i(x;y)\) or \(\mathrm{pmi}(x;y)\).
Averaging over all possible values of \(x\) and \(y\), the mutual information between the random variables is:
Thus, if \(X\) and \(Y\) are independent, they share zero mutual information, confirming that knowing \(Y\) does not reduce uncertainty about \(X\).
Mutual Information Under Full Dependence#
When \(\{Y = y\}\) completely determines \(\{X = x\}\), meaning that
the mutual information reduces to:
This is precisely the self-information of \(\{X = x\}\), indicating that when \(\{Y = y\}\) fully determines \(X\), the amount of information gained about \(X\) is equal to its own self-information.
The average mutual information is then:
Since the joint probability can be rewritten using the chain rule:
and given that \(Y\) is a deterministic function of \(X\), summing over \(y\) for each \(x\) gives:
This expression defines entropy, a fundamental measure of uncertainty.
Definition of Entropy#
The entropy of a discrete random variable \(X\), denoted \(H(X)\), quantifies the average uncertainty in its outcomes:
Entropy is the expected self-information of \(X\), representing how unpredictable the variable is on average. It depends solely on the probability distribution of \(X\), not the actual values of \(x\).
We can see that:
Higher entropy means greater uncertainty in \(X\)’s outcomes.
Lower entropy means less uncertainty, with entropy reaching zero if \(X\) is completely predictable (i.e., if one outcome has probability 1).
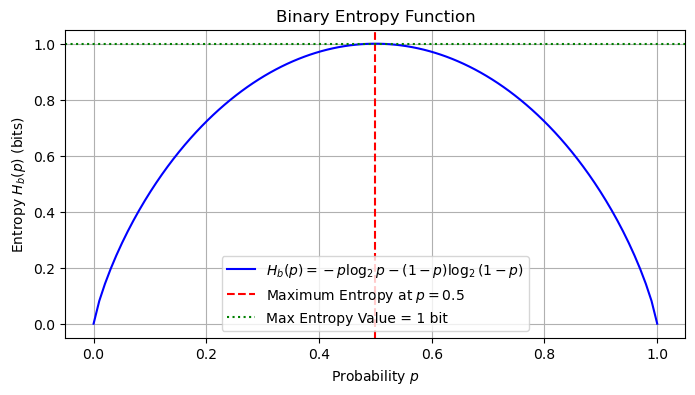
Example: Binary Entropy Function#
For a binary random variable \(X\) with outcomes \(\{0,1\}\) and probabilities:
the entropy is:
This function, called the binary entropy function \(H_b(p)\), is critical in coding theory and digital communication. It has the following properties:
Maximum entropy: \(H_b(p)\) peaks at 1 bit when \(p = 0.5\) (base 2), meaning that when the two outcomes are equiprobable, uncertainty is maximal.
Minimum entropy: \(H_b(p) = 0\) when \(p = 0\) or \(p = 1\), meaning that when one outcome is certain, uncertainty is zero.
This behavior reflects the fundamental principle that more balanced probabilities create greater uncertainty, while more skewed probabilities (favoring one outcome) reduce entropy.
import numpy as np
import matplotlib.pyplot as plt
# Define the binary entropy function
def binary_entropy(p):
"""Compute the binary entropy H_b(p) = -p log p - (1 - p) log (1 - p)."""
if p == 0 or p == 1:
return 0 # Define explicitly to avoid log(0) issues
return -p * np.log2(p) - (1 - p) * np.log2(1 - p)
# Generate probability values from 0 to 1
p_values = np.linspace(0, 1, 100)
entropy_values = np.array([binary_entropy(p) for p in p_values])
# Plot the binary entropy function
plt.figure(figsize=(8, 4))
plt.plot(p_values, entropy_values, label=r'$H_b(p) = -p \log_2 p - (1 - p) \log_2 (1 - p)$', color='b')
plt.axvline(x=0.5, linestyle='--', color='r', label='Maximum Entropy at $p=0.5$')
plt.axhline(y=1, linestyle=':', color='g', label='Max Entropy Value = 1 bit')
# Labels and legend
plt.xlabel('Probability $p$')
plt.ylabel('Entropy $H_b(p)$ (bits)')
plt.title('Binary Entropy Function')
plt.legend()
plt.grid(True)
# Show the plot
plt.show()
Interpretation of Entropy#
Entropy as a Measure of Information#
Entropy \(H(X)\) quantifies the average information content per source output.
Since observing \(X\) completely removes its uncertainty, entropy represents the expected information gained by resolving \(X\)’s ambiguity.
The unit of entropy depends on the logarithmic base:
Base 2 (bits): Common in digital communication, where 1 bit represents the information gained from a binary decision.
Base \(e\) (nats): Often used in theoretical contexts due to its natural logarithm properties.
By convention, the term \(0 \log 0\) is defined as 0, using the limit:
This ensures that entropy remains well-defined even when certain probabilities approach zero.
Dependence on Probabilities#
Entropy depends only on the probability distribution \(P[X = x]\), not the actual values of \(x\).
For example, if two sources have the same probability distribution but different symbols, such as:
\(\mathcal{X} = \{0,1\}\) with \(P[0] = 0.6, P[1] = 0.4\)
\(\mathcal{X} = \{A, B\}\) with \(P[A] = 0.6, P[B] = 0.4\)
their entropy values will be identical.
This highlights that entropy measures statistical uncertainty, not the semantic meaning of symbols.
Deterministic Source#
For a deterministic source, where one outcome occurs with certainty (\(P[X = x_0] = 1\)) and all others have zero probability:
Since \(P[x_0] = 1\) and \(\log 1 = 0\), and all other terms vanish, we get:
This confirms that if an outcome is certain, there is no uncertainty, and thus no information is gained from observing it.
Maximum Entropy for Equiprobable Outcomes#
Entropy is maximized when all outcomes are equiprobable.
For a discrete memoryless source (DMS) with \(|\mathcal{X}|\) symbols, where:
entropy simplifies to:
Since each term is the same, we factor out the sum:
This represents the greatest possible uncertainty, occurring when all outcomes are equally likely.
For example, for a fair coin (\(|\mathcal{X}| = 2\)):
This means that when outcomes are maximally uncertain, entropy reaches its peak value, requiring the most information to resolve uncertainty.
Properties of Entropy Functions#
Bounds on Entropy#
Entropy is always non-negative and has an upper bound:
Lower bound: Since probabilities satisfy \(0 < P[X = x] \leq 1\), we have
\[ -\log P[X = x] \geq 0. \]This ensures that \(H(X) \geq 0\), with equality only when \(X\) is deterministic (i.e., one outcome occurs with probability 1).
Upper bound: The maximum entropy occurs when all outcomes are equiprobable,
\[ P[X = x] = \frac{1}{|\mathcal{X}|} \quad \text{for all } x \in \mathcal{X}. \]In this case,
\[ H(X) = \log |\mathcal{X}|. \]This represents maximum uncertainty, as all symbols are equally likely.
Self-Mutual Information#
The mutual information of a variable with itself equals its entropy:
Since \(P[x \mid x] = 1\), the self-information simplifies to:
\[ I(x; x) = -\log P[x]. \]Averaging over all values of \(X\) gives:
\[ I(X; X) = \sum_{x \in \mathcal{X}} P[X = x] (-\log P[X = x]) = H(X). \]
This confirms that a variable provides full information about itself.
Mutual Information Bound#
Mutual information is always bounded by the smaller entropy of the two variables:
Since \(I(X; Y)\) measures shared information, it cannot exceed the total uncertainty in either \(X\) or \(Y\).
If \(X\) completely determines \(Y\) (or vice versa), then \(I(X; Y) = H(Y)\) (or \(H(X)\), respectively).
If \(X\) and \(Y\) are independent, then \(I(X; Y) = 0\).
This bound reinforces the limit on how much knowing one variable can tell us about the other.
Entropy Reduction by Functions#
If \(Y\) is a deterministic function of \(X\), i.e.,
then:
A function maps multiple possible values of \(X\) to a single value of \(Y\), which cannot increase uncertainty.
The entropy of \(Y\) is reduced if different values of \(X\) map to the same \(Y\), since the number of distinct outcomes decreases.
Equality holds only if \(g(X)\) is invertible, meaning each \(Y\) uniquely corresponds to an \(X\) (i.e., a bijection).
This property is useful in data compression and signal processing, where transformations aim to reduce redundancy and minimize entropy.
Joint Entropy#
Definition of Joint Entropy#
The joint entropy of a pair of discrete random variables \( (X, Y) \) is defined as:
This measures the total uncertainty in the joint distribution of \(X\) and \(Y\), indicating how much information is required to describe both variables together.
If \(X\) and \(Y\) are independent, then \(P[X = x, Y = y] = P[X = x] P[Y = y]\), leading to:
\[ H(X, Y) = H(X) + H(Y). \]This reflects that knowing one variable does not provide any information about the other.
If \(X\) and \(Y\) are dependent, then:
\[ H(X, Y) < H(X) + H(Y). \]The joint entropy is smaller due to shared information, meaning that knowing one variable reduces uncertainty about the other.
Extension to Multiple Variables#
For \(n\) random variables, the joint entropy generalizes to:
This captures the uncertainty across multiple variables, which is useful in various contexts, such as:
Sequences of transmitted signals in communication systems.
Multivariate probability models, where multiple variables interact.
Sensor networks, where multiple sources of data contribute to decision-making.
Joint entropy plays a key role in information theory, particularly in data compression and channel capacity analysis, as it determines how much information needs to be encoded to represent multiple variables simultaneously.
Conditional Entropy#
Conditional Entropy Given a Specific Value#
The conditional entropy of \(Y\) given that \(\{X = x\}\) measures the remaining uncertainty in \(Y\) after knowing \(\{X = x\}\). It is defined as:
If \(X\) and \(Y\) are independent, then knowing \(\{X = x\}\) does not change the uncertainty of \(Y\), so \(H(Y \mid X) = H(Y)\).
If \(X\) fully determines \(Y\), meaning \(P[Y = y \mid X = x]\) is either 0 or 1, then \(H(Y \mid X) = 0\) because there is no remaining uncertainty in \(Y\).
This conditional entropy function provides a measure of how much information about \(Y\) remains uncertain given \(X\).
Average Conditional Entropy#
The overall conditional entropy \(H(Y \mid X)\) is the expectation of \(H(Y \mid X = x)\) over all possible values of \(X\):
Expanding \(H(Y \mid X = x)\), we obtain:
This measures the expected uncertainty in \(Y\) given \(X\), meaning it quantifies how much information about \(Y\) is still unknown after observing \(X\).
Key interpretations:
If \(X\) and \(Y\) are independent, then \(H(Y \mid X) = H(Y)\), because knowing \(X\) does not reduce uncertainty about \(Y\).
If \(X\) fully determines \(Y\), then \(H(Y \mid X) = 0\), because \(Y\) is completely predictable from \(X\).
If \(X\) partially determines \(Y\), then \(0 \leq H(Y \mid X) \leq H(Y)\), meaning some uncertainty remains after knowing \(X\).
This concept is crucial in communication theory, where conditional entropy helps measure how much uncertainty remains in a received signal after considering the transmitted signal, aiding in error correction and decoding.
Properties of Joint and Conditional Entropy#
Bounds on Conditional Entropy#
Conditional entropy satisfies the following bounds:
Lower bound: \(H(Y \mid X) = 0\) if \(X\) fully determines \(Y\), meaning that for each \(x\), \(P[Y = y \mid X = x]\) is either 0 or 1 (no uncertainty remains in \(Y\) after knowing \(X\)).
Upper bound: \(H(Y \mid X) = H(Y)\) if \(X\) and \(Y\) are independent, meaning that knowing \(X\) does not reduce uncertainty about \(Y\) (\(P[Y = y \mid X = x] = P[Y = y]\)).
This confirms that conditional entropy always reduces uncertainty but never increases it.
Joint Entropy Decomposition#
The joint entropy can be expressed in terms of individual and conditional entropies:
This decomposition follows from the definition of conditional entropy and reflects that the total uncertainty in \(X, Y\) can be split into the uncertainty in \(X\) plus the remaining uncertainty in \(Y\) given \(X\) (or vice versa).
An important inequality follows:
Equality holds if and only if \(X\) and \(Y\) are independent, in which case:
\[ H(Y \mid X) = H(Y) \quad \text{and} \quad H(X \mid Y) = H(X). \]If \(X\) and \(Y\) are dependent, then \(H(X, Y) < H(X) + H(Y)\) due to shared information.
This decomposition is fundamental in data compression and information flow analysis.
Mutual Information Relations#
Mutual information quantifies the reduction in uncertainty when one variable is known. It can be expressed as:
This shows that mutual information measures the uncertainty in \(X\) reduced by knowing \(Y\) (or vice versa). It is also related to joint entropy:
This formulation highlights that mutual information captures the overlap between \(H(X)\) and \(H(Y)\)—the shared information between the two variables.
If \(X\) and \(Y\) are independent, then:
\[ H(X, Y) = H(X) + H(Y) \quad \Rightarrow \quad I(X; Y) = 0. \]If \(X\) and \(Y\) are fully dependent, then:
\[ H(X, Y) = \max(H(X), H(Y)) \quad \Rightarrow \quad I(X; Y) = \min(H(X), H(Y)). \]
This relation is key in quantifying correlations in information theory, such as in channel capacity, error correction, and machine learning (feature relevance).
Chain Rules for Entropies#
Chain Rule#
For \(n\) random variables, the chain rule expresses joint entropy as the sum of individual and conditional entropies:
This decomposition shows that the total uncertainty in \(X_1, X_2, \dots, X_n\) can be broken down into:
The entropy of the first variable \(H(X_1)\).
The additional uncertainty introduced by each successive variable given all previous ones.
This rule is fundamental in sequential modeling, such as Markov processes and natural language processing, where each variable depends on prior observations.
Inequality with Individual Entropies#
Joint entropy satisfies the inequality:
This follows from the chain rule:
since conditioning cannot increase entropy.
Equality holds if and only if \(X_1, X_2, \dots, X_n\) are independent, meaning that knowledge of one variable provides no information about the others:
\[ H(X_1, X_2, \ldots, X_n) = H(X_1) + H(X_2) + \cdots + H(X_n). \]If \(X_i\) are dependent, then \(H(X_1, X_2, \ldots, X_n)\) is strictly less than the sum of individual entropies due to shared information.
This property is crucial in data compression, where reducing redundancy among dependent variables leads to more efficient encoding.
i.i.d. Case#
For independent and identically distributed (i.i.d.) random variables \(X_1, X_2, \dots, X_n\), the joint entropy simplifies to:
where \(H(X)\) is the entropy of a single variable. This follows because:
Independence ensures that joint entropy is simply the sum of individual entropies.
Identical distribution means each variable has the same entropy \(H(X)\).
This result is fundamental in information theory, particularly in source coding and data compression, where entropy scales linearly with the number of independent symbols in a message.
