Time Delay Estimation in AWGN

Time-delay estimation, also termed time-of-arrival (TOA) estimation, is a common problem in radar and communications.

In radar a pulse is emitted at the transmitter, and after reflection from a target it is received with a \(\tau\)-second roundtrip delay.

In general, the random variable \(\tau\) can assume a continuum of values, so that the continuous version of the received signal is assumed, i.e.,

\[ y(t) = as(t - \tau) + n(t) \]

Note that, in practice, discrete processing and sampling are often employed, with the continuous signal being approximated by interpolation of samples.

MAP Estimation

A MAP estimate can be obtained by solving the following equation

\[ \frac{a}{\sigma^2} \int_0^{T_I} \left[ y(t) - as(t - \tau) \right] \frac{\partial s(t - \tau)}{\partial \tau} dt + \frac{\partial}{\partial \tau} \ln p(\tau) = 0 \]

where \(T_I\) is the integration interval.

Note that the integration interval should be longer than the pulse interval but short enough to make a decision as rapidly as possible in order to avoid noise accumulation in the estimate.

ML Estimation

Assuming no knowledge of the a priori pdf \(p(\tau)\), or equivalently assuming that the pdf of \(\tau\) is uniformly distributed.

A ML estimate can be derived as a solution to the equation

\[ \int_0^{T_I} \left[ y(t) - as(t - \hat{\tau}_{ML}) \right] \frac{\partial s(t - \hat{\tau}_{ML})}{\partial \hat{\tau}_{ML}} dt = 0 \]

The transmitted signal \(s(t)\) is typically a symmetric pulse.

Note that the second term is the integral of a symmetric function multiplied by its derivative and is therefore zero.

Under this condition, the preceding equation can be written as

\[ \int_0^{T_I} y(t) \frac{\partial s(t - \hat{\tau}_{ML})}{\partial \hat{\tau}_{ML}} dt = 0 \]

This equation must be solved for the estimate \(\hat{\tau}_{ML}\).

Delay-Locked Loop (DLL)

A phased-locked loop (PLL) can be used to implement the time-delay estimate, as shown in Figure 11.13 [B2].

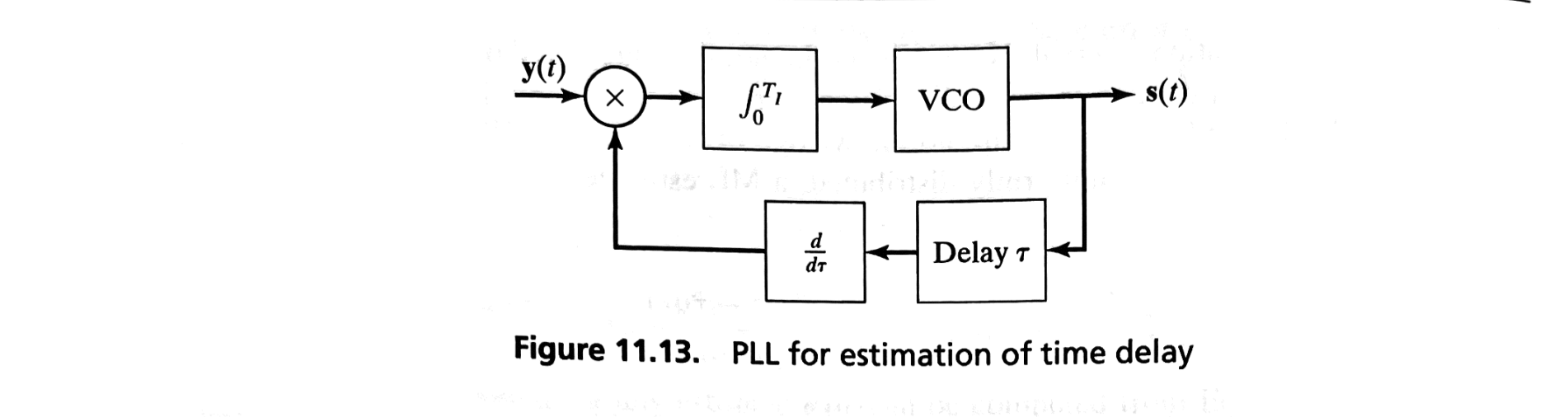
When a tracking loop is implemented in this fashion, it is often referred to as a delay-locked loop (DLL).

Cramér-Rao Bound and Minimum Variance

The Cramér-Rao bound for the delay estimate can be obtained in the case of an unbiased estimate by evaluating the minimum variance of the continuos case (introduced before) for amplitude estimation, i.e.,

\[ \sigma^2_{\text{min}}(\hat{\alpha}) = \frac{\sigma^2}{\int_0^T \left( \frac{\partial s(t, \alpha)}{\partial \alpha} \right)^2 dt} \]

with the assumption that the signal is zero outside the interval \((0, T)\), i.e.,

\[ \sigma^2_{\text{min}}(\hat{\tau}) = \frac{\sigma^2}{a^2 \int_{-\infty}^\infty \left[ \frac{\partial s(t - \tau)}{\partial \tau} \right]^2 dt} \]

To evaluate the previous equation let \(v(t) = \frac{\partial s(t - \tau)}{\partial \tau}\) and apply Parseval’s theorem, i.e.,

\[ \int_{-\infty}^\infty v^2(t) dt = \int_{-\infty}^\infty |V(f)|^2 df \]

where \(V(f)\) is the Fourier transform of \(v(t)\).

The Fourier transform \(V(f)\) is computed in terms of \(S(f)\), the Fourier transform of \(s(t)\), i.e.,

\[\begin{split} \begin{align*} V(f) &= \int_{-\infty}^\infty v(t)e^{-j2\pi ft} dt \\ &= \int_{-\infty}^\infty \frac{\partial s(t - \tau)}{\partial \tau} e^{-j2\pi ft} dt \\ &= \frac{\partial}{\partial \tau} \int_{-\infty}^\infty s(t - \tau)e^{-j2\pi ft} dt \\ &= \frac{\partial}{\partial \tau} e^{-j2\pi f \tau} S(f) \\ &= -j 2\pi f e^{-j2\pi f \tau} S(f) \end{align*} \end{split}\]

Combining above steps leads to

\[ \sigma^2_{\text{min}}(\hat{\tau}) = \frac{\sigma^2}{a^2 \int_{-\infty}^\infty (2\pi f)^2 |S(f)|^2 df} \]

Since the signal energy \(\mathcal{E}\) can be expressed as

\[ \mathcal{E} = \int_{-\infty}^\infty |S(f)|^2 df \]

Thus, \(\sigma^2_{\text{min}}(\hat{\tau})\) can be rewritten as

\[ \sigma^2_{\text{min}}(\hat{\tau}) = \frac{1}{a^2 B_s \mathcal{E} / \sigma^2} \]

where the parameter \(B_s\) is known as the effective bandwidth of the signal and is given by

\[ B_s = \frac{\int_{-\infty}^\infty (2\pi f)^2 |S(f)|^2 df}{\int_{-\infty}^\infty |S(f)|^2 df} \]

This result can be extended to narrowband signals rather than lowpass signals using complex lowpass equivalent representations.

Example: ML Estimation For Certain Signals

For certain signals an explicit representation of the estimate \(\hat{\tau}_{ML}\) can be obtained.

Consider the case

\[ s(t) = \sin 2\pi f_0 t \]

where \(f_0 = \frac{1}{T_0}\).

Then, the integral for ML estimation above, i.e.,

\[ \int_0^{T_I} y(t) \frac{\partial s(t - \hat{\tau}_{ML})}{\partial \hat{\tau}_{ML}} dt = 0 \]

becomes

\[ \int_0^{T_I} y(t) \cos 2\pi f_0(t - \hat{\tau}) dt = 0 \]

or

\[\begin{split} \begin{align*} &\cos 2\pi f_0 \hat{\tau} \int_0^{T_I} y(t) \cos 2\pi f_0 t \, dt \\ +\, &\sin 2\pi f_0 \hat{\tau} \int_0^{T_I} y(t) \sin 2\pi f_0 t \, dt = 0 \end{align*} \end{split}\]

or, solving for the estimate

\[ \hat{\tau}_{ML} = \frac{T_0}{2\pi} \tan^{-1} \left[ \frac{-\int_0^{T_I} y(t) \cos 2\pi f_0 t \, dt}{\int_0^{T_I} y(t) \sin 2\pi f_0 t \, dt} \right] \]

This equation is essentially that encountered in discrete form as a phase estimate.

Time-Delay Error

The time-delay error, \(\tau_e = \tau - \hat{\tau}_{ML}\), is related to the phase error by \(\tau_e = \frac{\theta_e}{2\pi f_0}\).

In the high-SNR case, \(\tau_e\) is a zero-mean, Gaussian random variable with a variance given by

\[ \sigma^2_{\tau_e} = \frac{1}{(2\pi f_0)^2} \frac{1}{a^2 \mathcal{E} / \sigma^2}. \]

Therefore, the delay estimate is unbiased and, for high signal-to-noise ratio, is efficient.

Matlab Example

• Group Delay Estimation in Simulink