Amplitude Estimation in the Noncoherent Case with AWGN#
In this section, we consider a sinusoidal signal with an unknown carrier phase \( \theta \), uniformly distributed over the interval \( (0, 2\pi) \).
The observed signal is expressed as:
where
\( f_0 \) represents the carrier frequency,
\( T_s \) is the sampling interval.
This setup corresponds to noncoherent Pulse Amplitude Modulation (PAM).
The parameter to be estimated is the amplitude \( a \), which may be treated either as a random variable or as an unknown deterministic scalar.
It is important to note that, in this context, the amplitude \( a \) is assumed to be nonnegative.
The A Posteriori PDF#
The goal is to determine the a posteriori probability density function (PDF) \( p(a | \vec{y}) \), which represents the probability distribution of the amplitude \( a \) given the observed data \( \vec{y} = [y_1, y_2, \ldots, y_k] \).
The derivation begins by calculating the likelihood function \( p(\vec{y} | a, \theta) \), which quantifies the probability of observing \( \vec{y} \) for a given amplitude \( a \) and phase \( \theta \).
Since the phase \( \theta \) is unknown and uniformly distributed, the a posteriori PDF is obtained by integrating (or averaging) the likelihood function over the possible values of \( \theta \), weighted by its uniform distribution.
Likelihood Function \( p(\vec{y} | a, \theta) \)
The additive noise \( n_i \) is modeled as zero-mean white Gaussian noise with variance \( \sigma^2 \).
The noise is independent and identically distributed (i.i.d.) across observations.
The likelihood expression is derived as:
where \( \beta = 2\pi f_0 T_s \) is a constant.
From the above likelihood function, the term inside the summation \( [y_i - a \sin(\beta i + \theta)]^2 \) can be expanded as:
Substituting this expansion back into the exponential:
The summation can now be split into three separate components:
Substituting this into the exponential:
We focus on isolating terms that depend on \( a \) and \( \theta \).
Notice that \( \sum_{i=1}^k y_i^2 \) does not depend on \( a \) or \( \theta \), so it can be separated as a constant term:
where \( \kappa_1 \) is the normalization factor:
To derive this step, we will use the trigonometric identity \( \sin^2 v = \frac{1}{2} - \frac{1}{2} \cos 2v \) to expand the term involving \( \sin^2(\beta i + \theta) \) in the likelihood function.
Dealing with \( \sin^2(\beta i + \theta) \)
Using the trigonometric identity:
we substitute this into the summation \( \sum_{i=1}^k \sin^2(\beta i + \theta) \):
Separating the terms:
Thus, the second term in the exponential becomes:
Simplify further:
Dealing with \( \sum_{i=1}^k y_i \sin(\beta i + \theta) \)
Using the trigonometric angle sum identity \( \sin(\beta i + \theta) = \sin(\beta i) \cos\theta + \cos(\beta i) \sin\theta \), the term \( \sum_{i=1}^k y_i \sin(\beta i + \theta) \) can be rewritten as:
Define the following terms:
This allows us to rewrite:
Substituting this back into the first term of the exponential:
Substituting the results into the likelihood function:
Simplifying the Double Frequency Term
The expression for \( p(\vec{y}|a, \theta) \) before this step includes the term:
This term represents the summation of a cosine function with a double frequency component \( 2\beta i \).
When \( k \) is large, and the phase terms \( 2\beta i + 2\theta \) are spread evenly across the interval, the sum of these cosine terms oscillates around zero, averaging out to approximately zero.
Thus, we neglect this term:
After removing this term, the likelihood function becomes:
Combining the First Two Terms in the Exponent
The first two terms in the exponent are:
This expression can be rewritten using the trigonometric identity for the cosine of a difference:
where:
Here, substitute \( x_1 = y_I \) and \( x_2 = y_Q \), so:
with:
Define:
Thus, the expression becomes:
The likelihood function now becomes:
\( p(\vec{y}|a) \) can be computed by averaging over the phase distribution, i.e.,
where again we have used
A MAP estimate can be obtained by using Bayes’ theorem in conjunction the likelihood above, so that
where \( \kappa_2 = \kappa_1 / p(\vec{y}) \).
Computing \( p(\vec{y}|a) \) by Averaging Over \( \theta \)
The likelihood \( p(\vec{y}|a) \) is obtained by averaging \( p(\vec{y}|a, \theta) \) over the uniform distribution of the unknown phase \( \theta \), which is uniformly distributed in \( [0, 2\pi) \).
This means we integrate \( p(\vec{y}|a, \theta) \) over \( \theta \), weighted by the uniform probability density \( \frac{1}{2\pi} \):
Substituting the form of \( p(\vec{y}|a, \theta) \) from the previous step:
we write:
Since \( \kappa_1 \) and \( \exp\left(-\frac{a^2 k}{4\sigma^2}\right) \) do not depend on \( \theta \), they can be factored out of the integral:
The integral inside is a standard form for the modified Bessel function of the first kind, \( I_0(u) \), which is defined as:
Here, \( u = \frac{a y_E}{\sigma^2} \). Substituting this into the expression for \( p(\vec{y}|a) \), we get:
Using Bayes’ Theorem to Compute \( p(a|\vec{y}) \)
The posterior \( p(a|\vec{y}) \) is obtained using Bayes’ theorem:
Substituting \( p(\vec{y}|a) \) into Bayes’ theorem:
Let:
Then:
Different from the coherent case, the pdf \( p(a|\vec{y}) \) is not a symmetric function of \( a \), so that the MAP, ML, and MSE are, in general, different.
The MAP estimate can be obtained by maximizing \( \ln p(a|\vec{y}) \), i.e.,
Solving for \( a \) in the foregoing equation results in \( \hat{a}_{MAP} \).
Key Differences from the Coherent Case
In the coherent case as in the previous section, the posterior probability density function (PDF) \( p(a|\vec{y}) \) is often symmetric with respect to \( a \), simplifying the estimation processes.
Symmetry implies that various estimates like the Maximum A Posteriori (MAP), Maximum Likelihood (ML), and Minimum Mean-Squared Error (MMSE) estimators may coincide.
In the noncoherent case, however:
The PDF \( p(a|\vec{y}) \) is not symmetric because of the phase averaging introduced by the integration over \( \theta \) and the nature of the modified Bessel functions.
This asymmetry means that the locations of the MAP, ML, and MMSE estimates generally differ.
MAP Estimation#
The MAP estimate, \( \hat{a}_{MAP} \), maximizes the posterior PDF \( p(a|\vec{y}) \).
To simplify this optimization, we maximize the logarithm of the posterior \( \ln p(a|\vec{y}) \) instead of \( p(a|\vec{y}) \) itself.
From Bayes’ theorem:
we take the logarithm:
Ignoring constants like \( \ln \kappa_2 \) (independent of \( a \)), the derivative with respect to \( a \) is:
Derivative of \( \ln I_0 \)
The term \( \frac{d}{da} \ln I_0\left(\frac{a y_E}{\sigma^2}\right) \) uses the known property of the modified Bessel function \( I_0(u) \):
Thus, for \( u = \frac{a y_E}{\sigma^2} \):
MAP Condition
Substituting these components into the derivative of \( \ln p(a|\vec{y}) \), we get:
Setting this derivative equal to zero yields the condition for the MAP estimate \( \hat{a}_{MAP} \):
Numerical Solution
Solving this equation for \( \hat{a}_{MAP} \) typically requires numerical methods, as the equation involves the modified Bessel functions \( I_0 \) and \( I_1 \), which are not simple to invert analytically.
The result, \( \hat{a}_{MAP} \), will depend on the observed data \( y_E \), the noise variance \( \sigma^2 \), the prior \( p(a) \), and the number of samples \( k \).
Example: Rayleigh Fading Amplitude Non-coherent Estimation#
As an example [Ex 11.3], assume that \( p(a) \) is a Rayleigh random variable.
This distribution is common in fading environments, as the amplitude of a received signal in Rayleigh fading results from the square root of the sum of squares of two independent Gaussian random variables (representing in-phase and quadrature components).
Rayleigh Prior for \( p(a) \)
The amplitude \( a \) is assumed to follow a Rayleigh distribution:
where \( \sigma_a^2 \) is the variance parameter of the Rayleigh distribution.
The logarithm of the prior \( p(a) \) is:
Differentiating \( \ln p(a) \) with respect to \( a \), we get:
MAP Estimation Equation
The general MAP estimation condition is given by:
Substituting \( \frac{d}{da} \ln p(a) = \frac{1}{a} - \frac{a}{\sigma_a^2} \), this becomes:
Simplifying the Energy Term \( \mathcal{E} \)
The term \( \mathcal{E} = \sum_{i=1}^k \sin^2(\beta i + \theta) \) represents the energy of the sinusoidal components.
Using the trigonometric identity \( \sin^2(x) = \frac{1}{2} - \frac{1}{2} \cos(2x) \), and assuming uniform phase distribution \( \theta \), the cosine terms average out to zero when summed over \( k \) samples. Thus:
This simplification allows us to replace \( k \) in the penalty term as \( a \mathcal{E} / \sigma^2 \), leading to the final MAP equation:
where \( \mathcal{E} = \frac{k}{2} \).
To address this equation, we consider the two following cases.
High-SNR Assumption#
The key assumption here is that the argument of the modified Bessel functions becomes large, i.e.,
This situation corresponds to high Signal-to-Noise Ratio (SNR), where the observed data \( y_E \) is much larger relative to the noise variance \( \sigma^2 \).
Simplifying the Bessel Function Ratio
For large arguments \( x \gg 1 \), the modified Bessel functions \( I_0(x) \) and \( I_1(x) \) behave asymptotically as:
Therefore, their ratio simplifies to:
Simplifying the MAP Equation
The general MAP equation is:
Using \( \frac{I_1}{I_0} \approx 1 \) at high SNR, the equation reduces to:
Rearranging the MAP Equation
Rewriting the simplified equation for clarity:
Combining the terms proportional to \( a \), this becomes:
Multiply through by \( a \) to eliminate the denominator:
This is a quadratic equation in \( a \):
where:
\( A = \frac{\mathcal{E}}{\sigma^2} + \frac{1}{\sigma_a^2} \)
\( B = \frac{y_E}{\sigma^2} \).
Solving the Quadratic Equation
The solution to the quadratic equation \( A a^2 - B a - 1 = 0 \) is given by:
Substituting \( -(-B) = B \) and simplifying:
Choosing the positive root (since \( a \geq 0 \) by definition):
Substituting \( A \) and \( B \) back into the equation:
we get that the high-SNR MAP estimate is:
At high SNR, we can see that the MAP estimate is influenced more by the observed data \( y_E \) and less by noise or prior assumptions.
Low-SNR Assumption#
In the low-SNR regime:
which corresponds to situations where the observed data \( y_E \) is small relative to the noise variance \( \sigma^2 \).
This happens with high probability at small SNR values, where noise dominates the signal.
Simplifying the Bessel Function Ratio
For small arguments \( x \ll 1 \), the modified Bessel functions \( I_0(x) \) and \( I_1(x) \) can be approximated by their Taylor series expansions:
Thus, the ratio becomes:
where the denominator \( 1 + \frac{x^2}{4} \) is approximated as \( 1 \) for very small \( x \).
Substituting \( x = \frac{a y_E}{\sigma^2} \), we get:
Simplifying the MAP Equation
The general MAP equation is:
Substitute \( \frac{I_1}{I_0} \approx \frac{a y_E}{2 \sigma^2} \):
Reorganizing terms gives:
Multiply through by \( a \) to eliminate the denominator:
Solving for \( a^2 \), we get:
Thus, the low-SNR MAP estimate is:
Constraint on \( y_E \)
For the denominator to remain positive, the following condition must hold:
Rearranging:
Simplify further:
This condition ensures that the estimate is valid.
We can see that at low SNR, the estimate is dominated by the prior information (\( \frac{1}{\sigma_a^2} \)) and the noise properties (\( \frac{\mathcal{E}}{\sigma^2} \)), with a smaller contribution from the data (\( y_E \)) due to the weak signal.
Simulation#
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
# Number of samples
N = 100
# Known symbol amplitude
s = 1.0
# Desired SNR in decibels
SNR_dB = 100
# Rayleigh distribution parameter (σ_a^2)
sigma_a_squared = 1.0
# Define SNR and Noise Variance
# Convert SNR from dB to linear scale
SNR_linear = 10 ** (SNR_dB / 10)
# Signal energy (since s is real and known)
E = s ** 2 # E = |s|^2 = 1.0
# Noise variance calculation based on SNR
sigma_squared = E / SNR_linear
# Generate True Amplitudes from Rayleigh Distribution
# In NumPy, the scale parameter for Rayleigh is σ_a = sqrt(σ_a^2 / 2)
sigma_a = np.sqrt(sigma_a_squared / 2)
# Sample true amplitudes from Rayleigh distribution
a_true = np.random.rayleigh(scale=sigma_a, size=N)
# Generate Noisy Observations
# Generate noise samples from Gaussian distribution N(0, σ²)
n = np.random.normal(loc=0.0, scale=np.sqrt(sigma_squared), size=N)
# Generate observations y = a * s + n
y = a_true * s + n
# Compute MAP Estimates
# Compute y_E = y^2 (Energy of the observation)
y_E = y ** 2
# Compute denominator of the MAP estimator
denominator_high_SNR = 2 * (E / sigma_squared + 1 / sigma_a_squared)
# Compute the argument inside the square root to ensure it's non-negative
sqrt_argument_high_SNR = (y_E / sigma_squared) ** 2 + 4 * (E / sigma_squared + 1 / sigma_a_squared)
# Compute the square root term
sqrt_term_high_SNR = np.sqrt(sqrt_argument_high_SNR)
# Compute the numerator of the MAP estimator
numerator_high_SNR = (y_E / sigma_squared) + sqrt_term_high_SNR
# Compute the MAP estimate for each observation
a_map_high_SNR = numerator_high_SNR / denominator_high_SNR
# Plotting True vs Estimated Amplitudes
# Generate sample indices for the x-axis
indices = np.arange(1, N + 1)
# Create a figure for True vs Estimated Amplitudes
plt.figure(figsize=(14, 7))
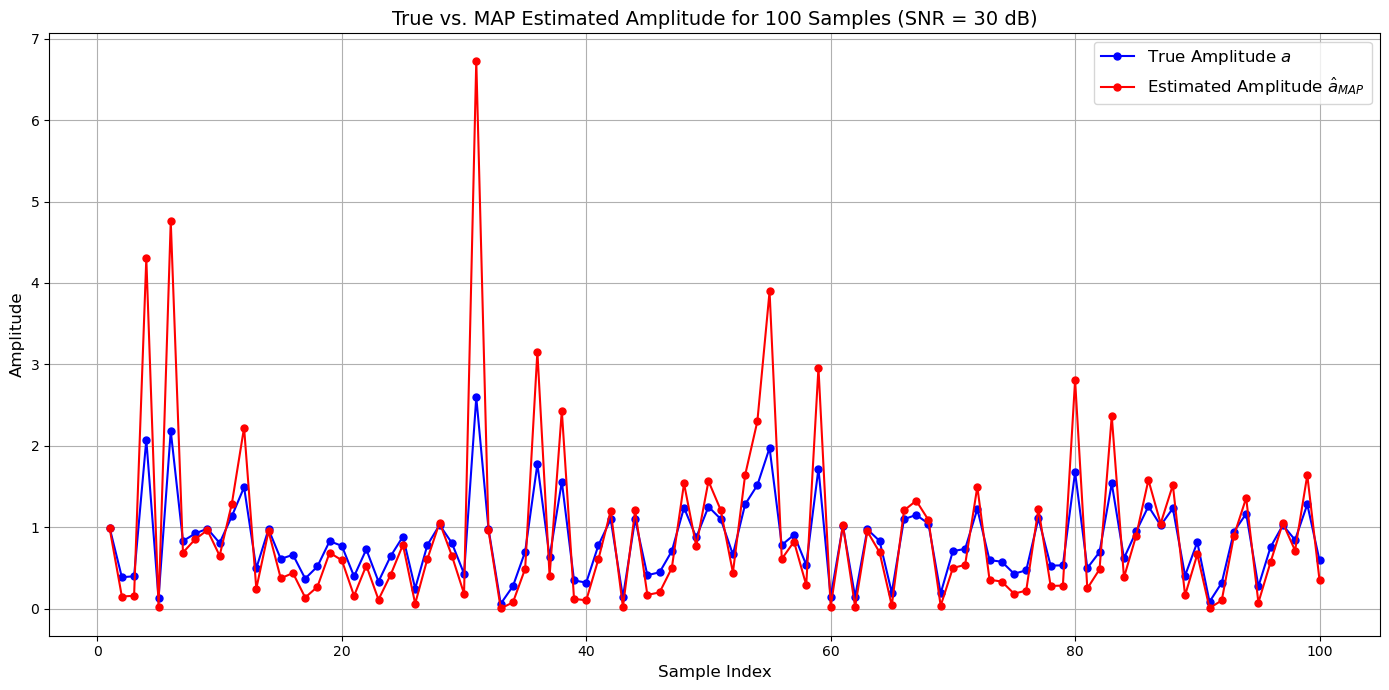
plt.plot(indices, a_true, 'bo-', label='True Amplitude $a$', markersize=5)
plt.plot(indices, a_map_high_SNR, 'ro-', label='Estimated Amplitude $\hat{a}_{MAP}$', markersize=5)
plt.xlabel('Sample Index', fontsize=12)
plt.ylabel('Amplitude', fontsize=12)
plt.title('True vs. MAP Estimated Amplitude for 100 Samples (SNR = 30 dB)', fontsize=14)
plt.legend(fontsize=12)
plt.grid(True)
plt.tight_layout()
plt.show()
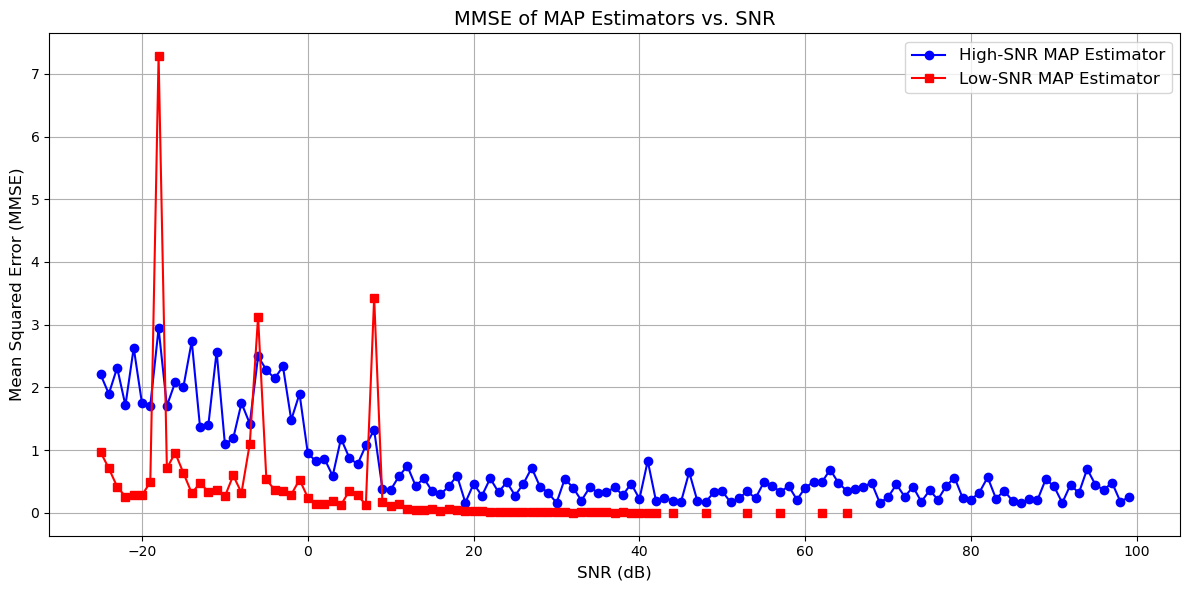
MMSE#
# SNR range in dB (0 dB to 40 dB in 1 dB steps)
SNR_dB_range = np.arange(-25, 100, 1) # [0, 1, 2, ..., 40]
# Initialize lists to store MMSE for each estimator and SNR
MMSE_high_SNR_list = []
MMSE_low_SNR_list = []
# Loop Over SNR Values
for SNR_dB in SNR_dB_range:
# Define SNR and Noise Variance
# Convert SNR from dB to linear scale
SNR_linear = 10 ** (SNR_dB / 10)
# Signal energy (since s is real and known)
E = s ** 2 # E = |s|^2 = 1.0
# Noise variance calculation based on SNR
sigma_squared = E / SNR_linear
# Generate True Amplitudes from Rayleigh Distribution
# In NumPy, the scale parameter for Rayleigh is σ_a = sqrt(σ_a^2 / 2)
sigma_a = np.sqrt(sigma_a_squared / 2)
# Sample true amplitudes from Rayleigh distribution
a_true = np.random.rayleigh(scale=sigma_a, size=N)
# Generate Noisy Observations
# Generate noise samples from Gaussian distribution N(0, σ²)
n = np.random.normal(loc=0.0, scale=np.sqrt(sigma_squared), size=N)
# Generate observations y = a * s + n
y = a_true * s + n
# Compute High-SNR MAP Estimates
# Compute y_E = y^2 (Energy of the observation)
y_E = y ** 2
# Compute denominator of the high-SNR MAP estimator
denominator_high = 2 * (E / sigma_squared + 1 / sigma_a_squared)
# Compute the argument inside the square root to ensure it's non-negative
sqrt_argument_high = (y_E / sigma_squared) ** 2 + 4 * (E / sigma_squared + 1 / sigma_a_squared)
# Ensure non-negativity
sqrt_argument_high = np.maximum(sqrt_argument_high, 0)
# Compute the square root term
sqrt_term_high = np.sqrt(sqrt_argument_high)
# Compute the numerator of the high-SNR MAP estimator
numerator_high = (y_E / sigma_squared) + sqrt_term_high
# Compute the high-SNR MAP estimate for each observation
a_map_high = numerator_high / denominator_high
# Compute Low-SNR MAP Estimates
# Compute the argument inside the square root for low-SNR MAP estimator
sqrt_argument_low = (E / sigma_squared) + (1 / sigma_a_squared) - 0.5 * (y_E / sigma_squared) ** 2
# To prevent invalid (negative) values inside the square root, set invalid entries to NaN
# and exclude them from the estimation
sqrt_argument_low_valid = np.where(sqrt_argument_low > 0, sqrt_argument_low, np.nan)
# Compute the square root term
sqrt_term_low = np.sqrt(sqrt_argument_low_valid)
# Compute the low-SNR MAP estimate
a_map_low = 1 / sqrt_term_low
# Calculate Estimation Errors and MMSE
# High-SNR Estimator Errors
errors_high = a_map_high - a_true
MMSE_high = np.mean(errors_high ** 2)
MMSE_high_SNR_list.append(MMSE_high)
# Low-SNR Estimator Errors
# Exclude NaN values resulting from invalid estimations
valid_indices_low = ~np.isnan(a_map_low)
errors_low = a_map_low[valid_indices_low] - a_true[valid_indices_low]
MMSE_low = np.mean(errors_low ** 2) if np.any(valid_indices_low) else np.nan
MMSE_low_SNR_list.append(MMSE_low)
# Plotting MMSE vs. SNR
plt.figure(figsize=(12, 6))
plt.plot(SNR_dB_range, MMSE_high_SNR_list, 'b-o', label='High-SNR MAP Estimator')
plt.plot(SNR_dB_range, MMSE_low_SNR_list, 'r-s', label='Low-SNR MAP Estimator')
plt.xlabel('SNR (dB)', fontsize=12)
plt.ylabel('Mean Squared Error (MMSE)', fontsize=12)
plt.title('MMSE of MAP Estimators vs. SNR', fontsize=14)
plt.grid(True)
plt.legend(fontsize=12)
plt.tight_layout()
plt.show()