Lossless Coding Algorithms#
Variable-Length Source Coding#
Variable-Length Coding for Unequal Probabilities#
When symbols in an information source occur with unequal probabilities, fixed-length coding becomes inefficient.
For example:
A source with four symbols could be encoded with 2-bit fixed-length codes (e.g., \(00, 01, 10, 11\)).
However, if one symbol appears far more frequently, using equal-length codes wastes bits.
Variable-length coding provides a solution:
Frequent symbols get shorter codewords.
Rare symbols get longer codewords.
This minimizes the average number of bits per symbol, improving compression efficiency.
This approach follows the principle of entropy coding: higher probability events require fewer bits to encode.
Example: Morse Code#
A historical example of variable-length coding is Morse code, developed in the 19th century for telegraphy.
In Morse code, letters are represented by dots (short signals) and dashes (long signals).
Frequently used letters receive shorter codes:
E → (·) (1 dot)
T → (–) (1 dash)
Less common letters receive longer codes:
Q → (––·–)
Z → (––··)
This design matches the probability distribution of English letters, reducing transmission time.
We can see that:
Morse code minimizes average transmission length by prioritizing brevity for frequent symbols.
This foreshadowed modern entropy-based coding, such as Huffman coding and arithmetic coding, which optimize data compression based on symbol frequencies.
This concept is foundational in efficient lossless compression for applications like file compression (ZIP, PNG) and data transmission.
Entropy Coding#
Probability-Based Code Word Assignment#
Following the principles of variable-length coding, entropy coding uses the probabilities of occurrence of source symbols to determine code word lengths.
The objective is to develop a systematic method for assigning code words that closely approach the theoretical minimum average length, as dictated by the entropy \(H(X)\) of the source.
Entropy coding aims to:
Assign shorter codes to high-probability symbols.
Assign longer codes to low-probability symbols.
Ensure that the average code length is as close as possible to \(H(X)\), in line with Shannon’s lossless coding theorem.
Example: Variable-Length Source Coding for DMS#
Consider a Discrete Memoryless Source (DMS) with four possible output symbols:
with the following probability distribution:
Letter |
\( P[a_k] \) |
Code I |
Code II |
Code III |
|---|---|---|---|---|
\( a_1 \) |
\( \frac{1}{2} \) |
1 |
0 |
0 |
\( a_2 \) |
\( \frac{1}{4} \) |
00 |
10 |
01 |
\( a_3 \) |
\( \frac{1}{8} \) |
01 |
110 |
011 |
\( a_4 \) |
\( \frac{1}{8} \) |
10 |
111 |
111 |
Calculating the Entropy of the Source#
The entropy of the source, assuming a base-2 logarithm (for measurement in bits), is computed as:
Substituting the given probabilities:
Thus, \(H(X) = 1.75\) bits, which represents the theoretical lower bound for the average number of bits per symbol in an optimal lossless coding scheme.
Evaluating the Code Efficiency#
To assess the efficiency of the three coding schemes, we compare their average code lengths to the entropy value:
Code I: \(1.50\) bits per symbol
Code II: \(1.75\) bits per symbol
Code III: \(1.75\) bits per symbol
Observations:
Code I has an average length of \(1.50\) bits, which is less than the source entropy (\(H(X) = 1.75\)). However, this suggests that Code I is not a valid prefix-free or uniquely decodable code, and therefore it cannot be used for reliable lossless compression.
Code II and Code III achieve the exact entropy value, making them optimal entropy codes that fully utilize the compression limit.
These findings demonstrate how variable-length codes can be designed to approach or exceed the theoretical limit, optimizing compression for a given source.
Instantaneous Codes#
Decodable Property and Flaws in Code I#
A code must be uniquely decodable, meaning any sequence of codewords can be unambiguously mapped back to the original source symbols.
Issue with Code I:
Although Code I follows a variable-length encoding scheme, it fails to be uniquely decodable.
Consider the encoded sequence: \(001001\)
The first two bits (00) decode to \(a_2\).
The remaining four bits (1001) cause ambiguity:
It could be split as \(10\) (\(a_4\)) and \(01\) (\(a_3\)).
Or it could be split as \(1\) (\(a_1\)), \(00\) (\(a_2\)), and \(1\) (\(a_1\)).
This ambiguity arises because:
The codeword for \(a_1\) (1) is a prefix of the codeword for \(a_4\) (10).
Without additional context (e.g., knowing the full length of a sequence), it is impossible to determine the correct decoding.
This violates the principle of unique decodability, making Code I impractical for reliable communication.
from typing import List, Dict
def encode(sequence: List[str], codebook: Dict[str, str]) -> str:
"""
Encodes a sequence of symbols based on the given codebook.
"""
return ''.join(codebook[symbol] for symbol in sequence)
def decode_ambiguities(encoded_sequence: str, codebook: Dict[str, str]) -> List[List[str]]:
"""
Attempt to decode a sequence in all possible ways based on the given codebook.
"""
reverse_codebook = {v: k for k, v in codebook.items()} # Reverse mapping
all_decodings = []
def decode_recursive(encoded: str, current_decoding: List[str]):
if not encoded:
all_decodings.append(current_decoding[:]) # Store a copy
return
# Try all possible code words
for code, letter in reverse_codebook.items():
if encoded.startswith(code):
decode_recursive(encoded[len(code):], current_decoding + [letter])
decode_recursive(encoded_sequence, [])
return all_decodings
# Define the codebook for Code I
codebook_I = {'a1': '1', 'a2': '00', 'a3': '01', 'a4': '10'}
# Example sequence to encode
sequence = ['a1', 'a2', 'a3', 'a4']
encoded_I = encode(sequence, codebook_I)
print("Encoded Sequence:", encoded_I)
# Given encoded sequence (demonstration case)
encoded_sequence_demo = "001001"
# Decode the sequence in all possible ways
all_possible_decodings = decode_ambiguities(encoded_sequence_demo, codebook_I)
# Print all possible decodings
for i, decoded_sequence in enumerate(all_possible_decodings, start=1):
print(f"Decoding {i}: {' '.join(decoded_sequence)}")
Encoded Sequence: 1000110
Decoding 1: a2 a1 a2 a1
Decoding 2: a2 a4 a3
Instantaneous Property and Decoding Delay#
One way to resolve the ambiguity in Code I is to wait for more bits (or use a delimiter), but this introduces decoding delay.
In real-time systems, where data needs to be interpreted immediately, such delays are undesirable.
An instantaneous code allows:
Immediate decoding of each codeword as soon as it is received, with no lookahead needed.
No ambiguity, because each codeword is distinguishable from all others.
Prefix-Free Codes#
Instantaneous codes must be prefix-free, meaning:
No codeword is a prefix of another.
This ensures that once a codeword is detected, decoding can proceed immediately.
Example of a Prefix-Free Code: \(\{0, 10, 110, 111\}\)
Here, no codeword starts with another codeword.
This allows for efficient, real-time decoding without ambiguity.
Thus, instantaneous codes are a practical necessity for applications such as telecommunications, real-time streaming, and data transmission protocols, ensuring efficient and error-free decoding.
Prefix Condition#
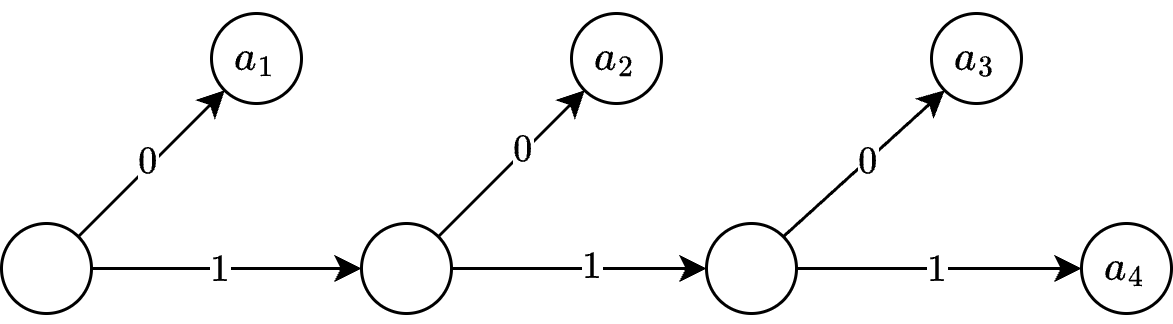
Instantaneous Decodability of Code II#
Code II is both uniquely decodable and instantaneous, meaning that it allows for immediate interpretation of each symbol without requiring additional context or lookahead.
For example, consider the encoded sequence: \(0101110\)
Decoding step-by-step:
(0) → \(a_1\) (next bit).
(10) → \(a_2\) (next bit).
(111) → \(a_4\) (next bit).
(0) → \(a_1\).
We can see that in Code II
Each codeword is instantly recognizable upon completion.
Once a valid codeword is read, the next symbol immediately starts without needing to store or analyze additional bits.
No codeword is a prefix of another.
Prefix-free structure ensures that:
\(0\) differs from \(10, 110, 111\)
\(10\) differs from \(110, 111\)
\(110\) differs from \(111\)
Because no codeword is a prefix of another, decoding remains instantaneous and unambiguous.
Significance:
Instantaneous decodability enables real-time applications where delay-free decoding is essential.
Prefix-free codes are self-synchronizing, meaning that even if a transmission error occurs, the decoder can quickly recover.
This principle is widely used in practical compression algorithms, including Huffman coding and prefix-free encoding schemes in modern file compression standards (e.g., PNG, MP3).
Thus, Code II follows the prefix condition, ensuring efficient and error-free decoding.
from typing import List, Dict
def encode(sequence: List[str], codebook: Dict[str, str]) -> str:
"""
Encodes a sequence of symbols based on the given codebook.
"""
return ''.join(codebook[symbol] for symbol in sequence)
def decode(encoded_sequence: str, codebook: Dict[str, str]) -> List[str]:
"""
Decodes an encoded sequence based on the given codebook.
"""
reverse_codebook = {v: k for k, v in codebook.items()} # Reverse mapping
decoded_sequence = []
buffer = ""
for bit in encoded_sequence:
buffer += bit
if buffer in reverse_codebook:
decoded_sequence.append(reverse_codebook[buffer])
buffer = ""
return decoded_sequence
# Define the codebook for Code II
codebook_II = {'a1': '0', 'a2': '10', 'a3': '110', 'a4': '111'}
# Example sequence to encode
sequence = ['a1', 'a2', 'a3', 'a4']
encoded_II = encode(sequence, codebook_II)
print("Encoded Sequence:", encoded_II)
# Decode the encoded sequence
decoded_II = decode(encoded_II, codebook_II)
print("Decoded Sequence:", ' '.join(decoded_II))
Encoded Sequence: 010110111
Decoded Sequence: a1 a2 a3 a4
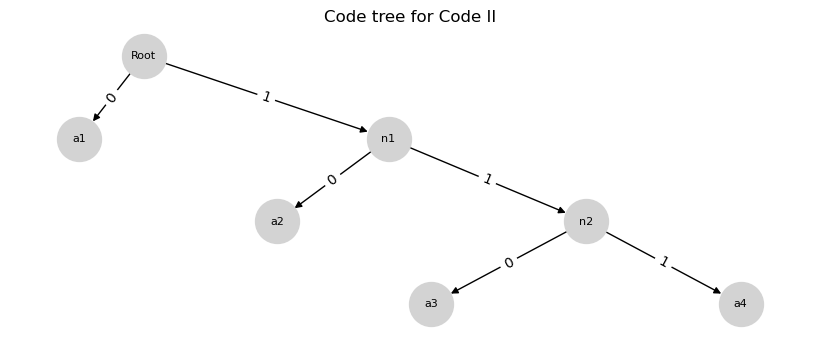
 Code tree for code II
Code tree for code II
import matplotlib.pyplot as plt
import networkx as nx
# Create a directed graph
G = nx.DiGraph()
# Define the tree structure with probabilities
edges = [
("Root", "a1", 0), ("Root", "n1", 1),
("n1", "a2", 0), ("n1", "n2", 1),
("n2", "a3", 0), ("n2", "a4", 1)
]
# Add nodes and edges
for parent, child, label in edges:
G.add_edge(parent, child, label=label)
# Positioning the nodes
pos = nx.drawing.nx_agraph.graphviz_layout(G, prog="dot")
# Draw the graph
plt.figure(figsize=(8, 3))
nx.draw(G, pos, with_labels=True, node_size=1000, node_color="lightgray", edge_color="black", font_size=8)
# Draw edge labels
edge_labels = {(parent, child): label for parent, child, label in edges}
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels, font_size=10)
# Show the diagram
plt.title("Code tree for Code II")
plt.show()
Definition of the Prefix Condition#
The prefix condition ensures that a code is instantaneously decodable, meaning that no codeword is a prefix of another.
Formal Definition:
For a codeword \( c_k \) of length \( k \) with bits:
no other codeword of length \( l < k \) can have the same initial segment:
Example: Code II
\(0\) (length 1) is not a prefix of \(10\), \(110\), or \(111\)
\(10\) (length 2) is not a prefix of \(110\) or \(111\)
Since no codeword starts with another, decoding can be immediate and unambiguous.
This guarantees unique and instantaneous decodability, as the decoder stops as soon as a valid codeword is formed.
Analysis of Code III#
While Code III is uniquely decodable, it is not instantaneous because it violates the prefix condition.
Example: Sequence \(0011\) Possible interpretations:
\(0\) (\(a_1\)) followed by \(011\) (\(a_3\)).
The decoder might need to wait to rule out \(01\) (\(a_2\)).
Prefix Condition Violation:
\(0\) is a prefix of \(01\).
\(01\) is a prefix of \(011\).
This forces the decoder to wait for additional bits, disqualifying Code III as instantaneous.
While prefix-free codes are always uniquely decodable, not all uniquely decodable codes are prefix-free — as demonstrated by Code III.
In addition, Code III allows unique decoding (by analyzing the full sequence), it requires lookahead or tree-based decoding, introducing delays.
def encode(sequence, codebook):
"""Encodes a sequence of symbols based on the given codebook."""
return ''.join(codebook[symbol] for symbol in sequence)
def decodeIII_final(encoded_sequence):
"""Decodes an encoded sequence based on Code III."""
reverse_codebook = {'0': 'a1', '01': 'a2', '011': 'a3', '111': 'a4'}
decoded_sequence = []
while encoded_sequence:
if encoded_sequence.endswith('111'):
decoded_sequence.insert(0, 'a4')
encoded_sequence = encoded_sequence[:-3]
elif encoded_sequence.endswith('011'):
decoded_sequence.insert(0, 'a3')
encoded_sequence = encoded_sequence[:-3]
elif encoded_sequence.endswith('01'):
decoded_sequence.insert(0, 'a2')
encoded_sequence = encoded_sequence[:-2]
elif encoded_sequence.endswith('0'):
decoded_sequence.insert(0, 'a1')
encoded_sequence = encoded_sequence[:-1]
else:
decoded_sequence.insert(0, 'Decoding Error')
break
return decoded_sequence
# Define the codebook
codebook_III = {'a1': '0', 'a2': '01', 'a3': '011', 'a4': '111'}
# Define the sequence
sequence = ['a3', 'a1', 'a2', 'a3', 'a4', 'a4']
# Encode the sequence
encoded_III = encode(sequence, codebook_III)
print("Encoded Sequence:", encoded_III)
# Example encoded test sequence
encodedTestSequenceIII = encoded_III # Replace with actual encoded sequence
# Decode the encoded sequence
decodedTestSequenceIIIFinal = decodeIII_final(encodedTestSequenceIII)
# Join and display the decoded sequence
decodedSequenceStr = ' '.join(decodedTestSequenceIIIFinal)
print("Decoded Sequence:", decodedSequenceStr)
Encoded Sequence: 011001011111111
Decoded Sequence: a3 a1 a2 a3 a4 a4
Average Length Comparison#
To assess the efficiency of Code II and Code III, we calculate their average lengths:
Code |
Equation |
Average Length |
|---|---|---|
Code II |
\( \frac{1}{2} \cdot 1 + \frac{1}{4} \cdot 2 + \frac{1}{8} \cdot 3 + \frac{1}{8} \cdot 3 \) |
1.75 bits |
Code III |
\( 0.5 \cdot 1 + 0.25 \cdot 2 + 0.125 \cdot 3 + 0.125 \cdot 3 \) |
1.75 bits |
Both codes match the entropy \(H(X) = 1.75\), meaning they are efficient.
However, Code II is superior because:
It achieves optimal compression while maintaining instantaneous decodability.
Code III requires lookahead, making it unsuitable for real-time applications.
Average Codeword Length#
Definition of Average Codeword Length#
For a variable-length coding scheme applied to a Discrete Memoryless Source (DMS) with \(L\) output symbols:
each symbol \( a_k \) is assigned a codeword of length \( n_k \) (bits) and occurs with probability \( P(a_k) \).
The average codeword length, denoted \( \bar{R} \), is the expected number of bits per source symbol, given by:
This represents the average rate of the code, where each codeword length is weighted by its probability of occurrence.
Example Calculation
Consider a DMS with two symbols:
\( a_1 \) has probability \( \frac{1}{2} \) and is assigned a 1-bit codeword (\(n_1 = 1\)).
\( a_2 \) has probability \( \frac{1}{2} \) and is assigned a 2-bit codeword (\(n_2 = 2\)).
The average codeword length is:
Objective of Efficient Code Design#
The primary objective in lossless coding is to develop a systematic method for constructing uniquely decodable variable-length codes that are efficient, meaning that the average codeword length \( \bar{R} \) is as small as possible.
A code is uniquely decodable if every sequence of codewords can be mapped back to a unique source sequence. Variable-length codes take advantage of unequal symbol probabilities to reduce \( \bar{R} \) below that of fixed-length codes.
Efficiency in coding means approaching the theoretical minimum set by the source’s entropy \( H(X) \), while balancing practicality (decodability) with optimality (minimal length).
Optimization Goal#
The objective in variable-length coding is to minimize \( \bar{R} \) while ensuring the code remains functional.
Ideally, \( \bar{R} \) should approach the entropy \(H(X)\) of the source, as per Shannon’s Source Coding Theorem.
Huffman coding and arithmetic coding are examples of techniques that aim to minimize \( \bar{R} \) while maintaining prefix-free and uniquely decodable properties.
By carefully selecting variable-length codes, we achieve efficient compression, reducing storage and transmission costs while ensuring decoding remains instantaneous and error-free.
The Kraft Inequality#
Statement of the Kraft Inequality#
The Kraft Inequality provides the condition under which a binary code with codeword lengths
(assumed ordered as \( n_1 \leq n_2 \leq \ldots \leq n_L \)) satisfies the prefix condition, ensuring that no codeword is a prefix of another, making the code instantaneously decodable.
The inequality states:
Each term \( 2^{-n_k} \) represents the fraction of the binary tree occupied by a codeword of length \( n_k \).
At level \( n_k \) in a binary tree, there are \( 2^{n_k} \) possible nodes.
The term \( 2^{-n_k} \) is the proportion of that level taken by one codeword.
The sum being \( \leq 1 \) ensures that the codewords can be placed in the tree without overlap, a necessary and sufficient condition for a prefix code.
Example (Valid Prefix Code)#
For codeword lengths \( \{1, 2, 2\} \) (e.g., \( \{0, 10, 11\} \)):
This satisfies the inequality, so a prefix code exists.
Counterexample (Invalid Prefix Code)#
For codeword lengths \( \{1, 1, 2\} \) (e.g., \( \{0, 1, 00\} \)):
Since the sum exceeds 1, no prefix code exists (e.g., \( 0 \) and \( 00 \) conflict).
Source Coding Theorem for Prefix Codes#
The Source Coding Theorem for Prefix Codes extends Shannon’s insight to practical code construction.
Theorem:#
Let \( X \) be a DMS with finite entropy \( H(X) \) and output symbols \( a_i \) (for \( 1 \leq i \leq N \)) with probabilities \( p_i \). It is possible to construct a prefix code with average length \( \bar{R} \) satisfying:
Key Bounds:
Lower Bound: \( \bar{R} \geq H(X) \)
This reflects Shannon’s First Theorem—entropy is the minimum average length for lossless coding.
Upper Bound: \( \bar{R} < H(X) + 1 \)
This guarantees that a prefix code exists with an average length within 1 bit of the entropy.
This bound is achievable using Huffman coding.
Example Application:
For a source with \( H(X) = 1.75 \) bits (as calculated earlier), a prefix code such as Code II: \( \{0, 10, 110, 111\} \) has an average length: \(\bar{R} = 1.75\).
This satisfies: \(1.75 \leq 1.75 < 2.75\).
Thus, Code II is optimal, as it matches the entropy lower bound while remaining a prefix code.
Coding Efficiency#
Definition of Coding Efficiency#
Let \( L_{\text{min}} \) be the minimum possible average codeword length for a source.
The coding efficiency of a source encoder is defined as:
Since no code can use fewer bits than the theoretical minimum (\( \bar{R} \geq L_{\text{min}} \)), it follows that:
An encoder is efficient when \( \eta \) approaches \(1\), meaning that the actual average codeword length \( \bar{R} \) is close to the theoretical minimum.
Example:
If the minimum possible length is:
and the actual average length is:
then:
This indicates 87.5% efficiency, meaning some redundancy remains in the coding scheme.
Determining \( L_{\text{min}} \) via Shannon’s Theorem#
The minimum possible average length (\( L_{\text{min}} \)) is determined by Shannon’s First Theorem, which states:
Entropy \( H(X) \) is the fundamental lower bound on the average number of bits per symbol in lossless compression.
No lossless code can achieve \( \bar{R} < H(X) \).
However, codes with \( \bar{R} > H(X) \) are possible.
Thus, setting:
we measure how close the code’s average length is to the entropy limit.
Example Calculations:
For \( H(X) = 1.75 \) and \( \bar{R} = 1.75 \) (Code II): \( \eta = \frac{1.75}{1.75} = 1.\) We have 100% efficiency—this is an optimal code.
For \( H(X) = 1.75 \) and \( \bar{R} = 2 \): \(\eta = \frac{1.75}{2} = 0.875\). We obtain less efficient—the code has extra redundancy.
Practical Implications#
The Kraft Inequality ensures that a prefix code exists.
The Source Coding Theorem guarantees that \( \bar{R} \) can approach \( H(X) \) within 1 bit.
Efficient codes (e.g., Huffman coding) minimize \( \bar{R} \) by assigning shorter codewords to more probable symbols, ensuring:
\[ \sum 2^{-n_k} \leq 1. \]
This bridges:
Theory: Entropy sets the lower limit.
Practice: Constructible codes approximate the entropy limit, enabling optimal lossless compression in practical applications like file compression (ZIP, PNG) and data transmission (error-free encoding).
