MAP Estimation for a Discrete Linear Observation Model#
The signal model described in previous section is continued in this section, i.e.,
\[
\vec{y} = H \vec{\alpha} + \vec{n}
\]
However, it is assumed here that the parameter vector is random, independent of the noise \(\vec{n}\), and with a Gaussian pdf represented as
\[
p(\vec{\alpha}) = \frac{1}{(2\pi)^{k/2} \text{det} A_{\alpha}^{1/2}} \exp\left( -\frac{1}{2} [\vec{\alpha} - \vec{\mu}_{\alpha}]^T A_{\alpha}^{-1} [\vec{\alpha} - \vec{\mu}_{\alpha}] \right)
\]
where \(\vec{\mu}_{\alpha}\) and \(A_{\alpha}\) are the mean and covariance matrix, respectively, of \(\vec{\alpha}\).
MAP Estimation#
A MAP estimate can be obtained for the vector \(\vec{\alpha}\) by computing
\[
\frac{\partial}{\partial \alpha_l} \ln p(\vec{y}|\vec{\alpha}) + \frac{\partial}{\partial \alpha_l} \ln p(\vec{\alpha}) = 0, \quad l = 1, \dots, L
\]
or in vector notation
\[
\frac{\partial}{\partial \vec{\alpha}} \ln p(\vec{y}|\vec{\alpha}) + \frac{\partial}{\partial \vec{\alpha}} \ln p(\vec{\alpha}) = 0
\]
The first term in this equation is computed as part of the ML estimate and is given by
\[
\frac{\partial}{\partial \vec{\alpha}} \ln p(\vec{y}|\vec{\alpha}) = H^T R_n^{-1} \vec{y} - H^T R_n^{-1} H \vec{\alpha}
\]
The second term is determined from the matrix identity
\[
\frac{\partial}{\partial \vec{v}} \left[ (\vec{v} - \vec{C}_v)^T P (\vec{v} - \vec{C}_v) \right] = [P + P^T] (\vec{v} - \vec{C}_v)
\]
where \(\vec{C}_v\) is a \(k\)-element real vector of constants.
With this identity, the second term becomes
\[\begin{split}
\begin{align*}
\frac{\partial}{\partial \vec{\alpha}} \ln p(\vec{\alpha})
&= \frac{\partial}{\partial \vec{\alpha}} \left[ -\frac{1}{2} (\vec{\alpha} - \vec{\mu}_{\alpha})^T A_{\alpha}^{-1} (\vec{\alpha} - \vec{\mu}_{\alpha}) \right] \\
&= -A_{\alpha}^{-1} (\vec{\alpha} - \vec{\mu}_{\alpha})
\end{align*}
\end{split}\]
since \((A_{\alpha}^{-1})^T = A_{\alpha}^{-1}\).
Combining these step, we have
\[\begin{split}
\begin{align*}
&\frac{\partial}{\partial \vec{\alpha}} \ln p(\vec{y}|\vec{\alpha}) + \frac{\partial}{\partial \vec{\alpha}} \ln p(\vec{\alpha}) \\
= \,
&H^T R_n^{-1} \vec{y} - H^T R_n^{-1} H \vec{\alpha} - A_{\alpha}^{-1} (\vec{\alpha} - \vec{\mu}_{\alpha}) \\
= \, &0
\end{align*}
\end{split}\]
The solution of this equation for \(\vec{\alpha}\) yields the MAP estimator
\[\boxed{
\vec{\hat{\alpha}}_{MAP} = (H^T R_n^{-1} H + A_{\alpha}^{-1})^{-1} (H^T R_n^{-1} \vec{y} + A_{\alpha}^{-1} \vec{\mu}_{\alpha})
}
\]
Note that the a posteriori pdf \(p(\vec{\alpha} | \vec{y})\) is Gaussian, so that the MAP and MSE estimates are the same.
Unbiased#
Using \(\mathbb{E}[\vec{y}] = \mathbb{E}[H \vec{\alpha}] = H \vec{\mu}_{\alpha}\), it can be seen that \(\vec{\hat{\alpha}}_{MAP}\) is unbiased.
That is:
\[\begin{split}
\begin{align*}
\mathbb{E}[\vec{\hat{\alpha}}_{MAP}]
&= (H^T R_n^{-1} H + A_{\alpha}^{-1})^{-1} (H^T R_n^{-1} \mathbb{E}[\vec{y}] + A_{\alpha}^{-1} \vec{\mu}_{\alpha}) \\
&= (H^T R_n^{-1} H + A_{\alpha}^{-1})^{-1} (H^T R_n^{-1} H \vec{\mu}_{\alpha} + A_{\alpha}^{-1} \vec{\mu}_{\alpha}) \\
&= \vec{\mu}_{\alpha}
\end{align*}
\end{split}\]
Example#
A numerical example [B2, Ex. 12.4] is provided to illustrate the nature of the computations.
Assume that the observables are related by
\[\begin{split}
\begin{align*}
\vec{y}_1 &= \alpha_1 + \alpha_3 + n_1 \\
\vec{y}_2 &= \alpha_1 + \alpha_2 + n_2
\end{align*}
\end{split}\]
where
\[\begin{split}
R_n =
\begin{bmatrix}
2 & 1 \\
1 & 1
\end{bmatrix}
\end{split}\]
\[\begin{split}
A_{\alpha} =
\begin{bmatrix}
2 & 1 & 0 \\
1 & 2 & 1 \\
0 & 1 & 1
\end{bmatrix}
\end{split}\]
\[\begin{split}
\vec{\mu}_{\alpha} =
\begin{bmatrix}
1 \\
0 \\
0
\end{bmatrix}.
\end{split}\]
Then, the following results can be obtained:
\[\begin{split}
H =
\begin{bmatrix}
1 & 0 & 1 \\
1 & 1 & 0
\end{bmatrix},
\end{split}\]
\[\begin{split}
R_n^{-1} =
\begin{bmatrix}
1 & -1 \\
-1 & 2
\end{bmatrix},
\end{split}\]
\[\begin{split}
A_{\alpha}^{-1} =
\begin{bmatrix}
1 & -1 & 1 \\
-1 & 2 & -2 \\
1 & -2 & 3
\end{bmatrix}.
\end{split}\]
From which it follows that
\[\begin{split}
\begin{align*}
H^TR_n^{-1}
&=
\begin{bmatrix}
1 & 1 \\
0 & 1 \\
1 & 0
\end{bmatrix}
\begin{bmatrix}
1 & -1 \\
-1 & 2
\end{bmatrix}
\\
&=
\begin{bmatrix}
0 & 1 \\
-1 & 2 \\
1 & -1
\end{bmatrix}
\end{align*}
\end{split}\]
\[\begin{split}
\begin{align*}
A_{\alpha}^{-1} \vec{\mu}_{\alpha}
&=
\begin{bmatrix}
1 & -1 & 1 \\
-1 & 2 & -2 \\
1 & -2 & 3
\end{bmatrix}
\begin{bmatrix}
1 \\
0 \\
0
\end{bmatrix}
\\
&=
\begin{bmatrix}
1 \\
-1 \\
1
\end{bmatrix}
\end{align*}
\end{split}\]
\[\begin{split}
\begin{align*}
H^TR_n^{-1}H + A_{\alpha}^{-1}
&=
\begin{bmatrix}
0 & 1 \\
-1 & 2 \\
1 & -1
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 1 \\
1 & 1 & 0
\end{bmatrix}
\\
&\quad+
\begin{bmatrix}
1 & -1 & 1 \\
-1 & 2 & -2 \\
1 & -2 & 3
\end{bmatrix}
\\
&=
\begin{bmatrix}
2 & 0 & 1 \\
0 & 4 & -3 \\
1 & -3 & 4
\end{bmatrix}
\end{align*}
\end{split}\]
\[\begin{split}
(H^TR_n^{-1}H + A_{\alpha}^{-1})^{-1} =
\frac{1}{10}
\begin{bmatrix}
7 & -3 & -4 \\
-3 & 7 & 6 \\
-4 & 6 & 8
\end{bmatrix}.
\end{split}\]
From Eq. (12.46) and the previous relationships, the MAP estimate is
\[\begin{split}
\begin{align*}
\hat{\vec{\alpha}}_{MAP}
&= \frac{1}{10}
\begin{bmatrix}
7 & -3 & -4 \\
-3 & 7 & 6 \\
-4 & 6 & 8
\end{bmatrix}
\begin{bmatrix}
0 & 1 \\
-1 & 2 \\
1 & -1
\end{bmatrix}
\begin{bmatrix}
y_1 \\
y_2
\end{bmatrix}
\\
&+
\frac{1}{10}
\begin{bmatrix}
7 & -3 & -4 \\
-3 & 7 & 6 \\
-4 & 6 & 8
\end{bmatrix}
\begin{bmatrix}
1 \\
-1 \\
1
\end{bmatrix}
\end{align*}
\end{split}\]
or
\[
\hat{\alpha}_{MAP,1} = -\frac{y_1}{10} + \frac{y_2}{2} + \frac{3}{5},
\]
\[
\hat{\alpha}_{MAP,2} = -\frac{y_1}{10} + \frac{y_2}{2} - \frac{2}{5},
\]
\[
\hat{\alpha}_{MAP,3} = \frac{y_1}{5} - \frac{1}{5}.
\]
Simulation#
We have that
\[\begin{split}
\begin{align*}
\hat{\alpha}_{MAP,1} &= -\frac{y_1}{10} + \frac{y_2}{2} + \frac{3}{5} \\
\hat{\alpha}_{MAP,2} &= -\frac{y_1}{10} + \frac{y_2}{2} - \frac{2}{5} \\
\hat{\alpha}_{MAP,3} &= \frac{y_1}{5} - \frac{1}{5}
\end{align*}
\end{split}\]
Write the MAP equations in matrix form (combine the terms involving \( y_1 \) and \( y_2 \) into a matrix multiplication, and separate the constant terms)
\[\begin{split}
\begin{bmatrix}
\hat{\alpha}_{MAP,1} \\
\hat{\alpha}_{MAP,2} \\
\hat{\alpha}_{MAP,3}
\end{bmatrix}
=
\begin{bmatrix}
-\frac{1}{10} & \frac{1}{2} \\
-\frac{1}{10} & \frac{1}{2} \\
\frac{1}{5} & 0
\end{bmatrix}
\begin{bmatrix}
y_1 \\
y_2
\end{bmatrix}
+
\begin{bmatrix}
\frac{3}{5} \\
-\frac{2}{5} \\
-\frac{1}{5}
\end{bmatrix}.
\end{split}\]
Define the components:
\[\begin{split}
\text{MAP estimator matrix} =
\begin{bmatrix}
-\frac{1}{10} & \frac{1}{2} \\
-\frac{1}{10} & \frac{1}{2} \\
\frac{1}{5} & 0
\end{bmatrix}.
\end{split}\]
\[\begin{split}
\text{MAP estimator offset} =
\begin{bmatrix}
\frac{3}{5} \\
-\frac{2}{5} \\
-\frac{1}{5}
\end{bmatrix}.
\end{split}\]
import numpy as np
import matplotlib.pyplot as plt
# Number of simulations
num_simulations = 100
# Define prior parameters
mu_alpha = np.array([1.0, 0.0, 0.0]) # mu_alpha = [1, 0, 0]
A_alpha = np.array([
[2, 1, 0],
[1, 2, 1],
[0, 1, 1]
])
# Compute the inverse of A_alpha
A_alpha_inv = np.linalg.inv(A_alpha)
# Define noise covariance matrix R_n and its inverse R_n_inv
R_n = np.array([
[2, 1],
[1, 1]
])
R_n_inv = np.linalg.inv(R_n)
# Define H matrix
H = np.array([
[1, 0, 1],
[1, 1, 0]
])
# Precompute H^T R_n_inv
Ht_Rn_inv = H.T @ R_n_inv # Shape: (3, 2)
# Compute H^T R_n_inv H + A_alpha_inv
Ht_Rn_H = Ht_Rn_inv @ H # Shape: (3, 3)
Ht_Rn_H_plus_Ainv = Ht_Rn_H + A_alpha_inv # Shape: (3, 3)
# Compute the inverse of (H^T Rn^{-1} H + A_alpha^{-1})
Ht_Rn_H_plus_Ainv_inv = np.linalg.inv(Ht_Rn_H_plus_Ainv) # Shape: (3, 3)
# Compute the MAP estimator matrix
# This involves multiplying (Ht_Rn_H + Ainv)^{-1} with (Ht_Rn_inv)
MAP_estimator_matrix = Ht_Rn_H_plus_Ainv_inv @ Ht_Rn_inv # Shape: (3, 2)
# Compute the term (Ht_Rn_H + Ainv)^{-1} A_alpha_inv mu_alpha
MAP_estimator_offset = Ht_Rn_H_plus_Ainv_inv @ A_alpha_inv @ mu_alpha # Shape: (3,)
# Initialize arrays to store true and estimated parameters
true_alpha = np.random.multivariate_normal(mean=mu_alpha, cov=A_alpha, size=num_simulations) # Shape: (num_simulations, 3)
alpha_estimates = np.zeros((num_simulations, 3)) # Columns: alpha1_est, alpha2_est, alpha3_est
# Perform simulations
for i in range(num_simulations):
# Current true alpha vector
alpha_current = true_alpha[i]
# Generate noise sample from multivariate normal distribution
noise = np.random.multivariate_normal(mean=np.zeros(2), cov=R_n) # [n1, n2]
# Generate measurements y1 and y2
y = H @ alpha_current + noise # Shape: (2,)
# Compute MAP estimates
alpha_map = MAP_estimator_matrix @ y + MAP_estimator_offset # Shape: (3,)
# Store estimates
alpha_estimates[i] = alpha_map
# Compute statistics
alpha_estimates_mean = np.mean(alpha_estimates, axis=0)
alpha_estimates_std = np.std(alpha_estimates, axis=0)
# Cramér-Rao Bounds (CRB)
# The posterior covariance matrix is (H^T Rn^{-1} H + A_alpha^{-1})^{-1}
posterior_covariance = Ht_Rn_H_plus_Ainv_inv # Shape: (3,3)
CRB_variances = np.diag(posterior_covariance) # Variances for alpha1, alpha2, alpha3
# Display results
print("True Parameters Prior:")
print(f"mu_alpha = {mu_alpha}")
print(f"A_alpha =\n{A_alpha}\n")
print("MAP Estimator Results (Mean ± Std Dev):")
print(f"alpha1_est = {alpha_estimates_mean[0]:.4f} ± {alpha_estimates_std[0]:.4f}")
print(f"alpha2_est = {alpha_estimates_mean[1]:.4f} ± {alpha_estimates_std[1]:.4f}")
print(f"alpha3_est = {alpha_estimates_mean[2]:.4f} ± {alpha_estimates_std[2]:.4f}\n")
print("Cramér-Rao Bounds (CRB):")
print(f"Var(alpha1) >= {CRB_variances[0]:.4f}")
print(f"Var(alpha2) >= {CRB_variances[1]:.4f}")
print(f"Var(alpha3) >= {CRB_variances[2]:.4f}\n")
# Visualization
# Create an array of indices
indices = np.arange(1, num_simulations + 1)
# Select a subset of indices for clearer plots (e.g., first 1000)
plot_subset = 1000
subset_indices = indices[:plot_subset]
subset_true_alpha1 = true_alpha[:plot_subset, 0]
subset_true_alpha2 = true_alpha[:plot_subset, 1]
subset_true_alpha3 = true_alpha[:plot_subset, 2]
subset_est_alpha1 = alpha_estimates[:plot_subset, 0]
subset_est_alpha2 = alpha_estimates[:plot_subset, 1]
subset_est_alpha3 = alpha_estimates[:plot_subset, 2]
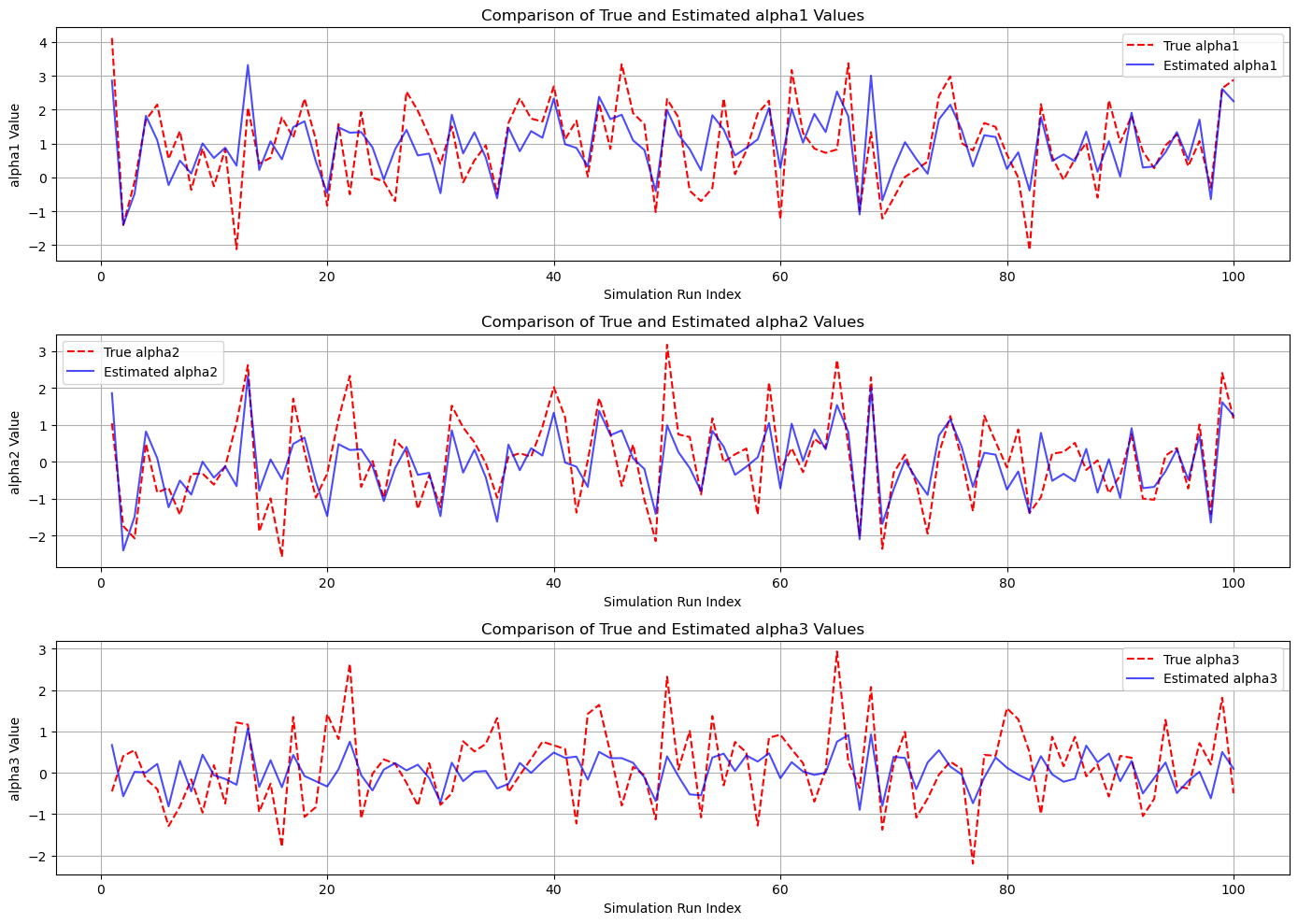
# Plot for alpha1
plt.figure(figsize=(14, 10))
plt.subplot(3, 1, 1)
plt.plot(subset_indices, subset_true_alpha1, label='True alpha1', color='red', linestyle='--')
plt.plot(subset_indices, subset_est_alpha1, label='Estimated alpha1', color='blue', alpha=0.7)
plt.title('Comparison of True and Estimated alpha1 Values')
plt.xlabel('Simulation Run Index')
plt.ylabel('alpha1 Value')
plt.legend()
plt.grid(True)
# Plot for alpha2
plt.subplot(3, 1, 2)
plt.plot(subset_indices, subset_true_alpha2, label='True alpha2', color='red', linestyle='--')
plt.plot(subset_indices, subset_est_alpha2, label='Estimated alpha2', color='blue', alpha=0.7)
plt.title('Comparison of True and Estimated alpha2 Values')
plt.xlabel('Simulation Run Index')
plt.ylabel('alpha2 Value')
plt.legend()
plt.grid(True)
# Plot for alpha3
plt.subplot(3, 1, 3)
plt.plot(subset_indices, subset_true_alpha3, label='True alpha3', color='red', linestyle='--')
plt.plot(subset_indices, subset_est_alpha3, label='Estimated alpha3', color='blue', alpha=0.7)
plt.title('Comparison of True and Estimated alpha3 Values')
plt.xlabel('Simulation Run Index')
plt.ylabel('alpha3 Value')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
True Parameters Prior:
mu_alpha = [1. 0. 0.]
A_alpha =
[[2 1 0]
[1 2 1]
[0 1 1]]
MAP Estimator Results (Mean ± Std Dev):
alpha1_est = 0.9594 ± 0.8941
alpha2_est = -0.0406 ± 0.8941
alpha3_est = 0.0503 ± 0.4038
Cramér-Rao Bounds (CRB):
Var(alpha1) >= 0.7000
Var(alpha2) >= 0.7000
Var(alpha3) >= 0.8000
# Define the MAP estimator matrix
MAP_estimator_matrix_theory = np.array([
[-1/10, 1/2],
[-1/10, 1/2],
[1/5, 0]
])
# Define the MAP estimator offset
MAP_estimator_offset_theory = np.array([
3/5,
-2/5,
-1/5
])
print(MAP_estimator_matrix)
print(MAP_estimator_matrix_theory)
print(MAP_estimator_offset)
print(MAP_estimator_offset_theory)
[[-1.00000000e-01 5.00000000e-01]
[-1.00000000e-01 5.00000000e-01]
[ 2.00000000e-01 1.11022302e-16]]
[[-0.1 0.5]
[-0.1 0.5]
[ 0.2 0. ]]
[ 0.6 -0.4 -0.2]
[ 0.6 -0.4 -0.2]
Example 12.5#
Assume that \(\alpha\) is Gaussian with zero mean and variance \(\sigma_\alpha^2\).
We wish to find the MAP estimate of \(\alpha\) given that
\[
\vec{y} = H\alpha + \vec{n}
\]
\[\begin{split}
H =
\begin{bmatrix}
1 \\
1
\end{bmatrix}
\end{split}\]
and \(\vec{n}\) is Gaussian with zero mean and covariance matrix
\[\begin{split}
R_n = \sigma^2
\begin{bmatrix}
1 & \rho \\
\rho & 1
\end{bmatrix}.
\end{split}\]
Using Eq. (12.46) with \(A_\alpha = \sigma_\alpha^2\),
\[\begin{split}
\begin{align*}
\hat{\alpha}_{MAP}
&= \Big( H^T R_n^{-1} H + A_\alpha^{-1} \Big)^{-1}
\Big( H^T R_n^{-1} \vec{y} + A_\alpha^{-1} \vec{\mu}_\alpha \Big)
\\
&= \Bigg[
\begin{bmatrix}
1 & 1
\end{bmatrix}
\begin{bmatrix}
\sigma^2 & \rho\sigma^2 \\
\rho\sigma^2 & \sigma^2
\end{bmatrix}^{-1}
\begin{bmatrix}
1 \\
1
\end{bmatrix}
+ \frac{1}{\sigma_\alpha^2} \Bigg]^{-1} \\
&\times
\Bigg[
\begin{bmatrix}
1 & 1
\end{bmatrix}
\begin{bmatrix}
\sigma^2 & \rho\sigma^2 \\
\rho\sigma^2 & \sigma^2
\end{bmatrix}^{-1}
\Bigg] \vec{y}
\\
&\times \Bigg[
\frac{2}{\sigma^2(1+\rho)}
+ \frac{1}{\sigma_\alpha^2}
\Bigg]^{-1}
\frac{
\begin{bmatrix}
1 & 1
\end{bmatrix}}
{\sigma^2(1+\rho)}
\vec{y}
\end{align*}
\end{split}\]
Thus, we have
\[\boxed{
\hat{\alpha}_{MAP} = \frac{\sigma_\alpha^2 (y_1 + y_2)}{2\sigma_\alpha^2 + \sigma^2(1+\rho)}.
}
\]
or
\[\begin{split}
\hat{\alpha}_{MAP} = \frac{\sigma_\alpha^2}{2\sigma_\alpha^2 + \sigma^2(1+\rho)}
\begin{bmatrix}
1 & 1
\end{bmatrix}
\begin{bmatrix}
y_1 \\
y_2
\end{bmatrix}.
\end{split}\]
import numpy as np
import matplotlib.pyplot as plt
# Set random seed for reproducibility
np.random.seed(42)
# Simulation parameters
N = 10000 # Number of simulations
sigma_alpha2 = 1 # Prior variance of alpha (σ_α²)
sigma2 = 1 # Noise variance (σ²)
rho = 0.5 # Correlation coefficient between noise in y1 and y2
mu_alpha = 0 # Prior mean of alpha (set to zero for N(0, σ_α²))
# Sample alpha_true from a Gaussian distribution N(mu_alpha, sigma_alpha2)
alpha_true = np.random.normal(loc=mu_alpha, scale=np.sqrt(sigma_alpha2), size=N)
# Define noise covariance matrix Rn and its inverse
Rn = np.array([
[sigma2, rho * sigma2],
[rho * sigma2, sigma2]
])
Rn_inv = np.linalg.inv(Rn)
# Compute denominator for the MAP estimator
denominator = 2 * sigma_alpha2 + sigma2 * (1 + rho)
# Compute MAP estimator coefficients
MAP_coefficient = sigma_alpha2 / denominator # Coefficient for y1 and y2
MAP_offset = (sigma2 * (1 + rho)) / denominator * mu_alpha # Offset incorporating prior mean
# Define MAP_estimator_matrix and MAP_estimator_offset based on corrected formula
MAP_estimator_matrix = np.array([MAP_coefficient, MAP_coefficient])
MAP_estimator_offset = MAP_offset # This will be zero since mu_alpha is zero
# Initialize arrays to store estimated alphas and observations
alpha_estimates = np.zeros(N)
y1_all = np.zeros(N)
y2_all = np.zeros(N)
# Perform simulations
for i in range(N):
# Generate noise sample from multivariate normal distribution
noise = np.random.multivariate_normal(mean=[0, 0], cov=Rn)
n1, n2 = noise
# Generate observations y1 and y2 using the randomly sampled alpha_true
y1 = alpha_true[i] + n1
y2 = alpha_true[i] + n2
# Store observations for potential visualization
y1_all[i] = y1
y2_all[i] = y2
# Observation vector
y = np.array([y1, y2])
# Compute MAP estimate using the corrected estimator
alpha_map = MAP_estimator_matrix @ y + MAP_estimator_offset # Equivalent to MAP_coefficient * (y1 + y2)
# Store the estimate
alpha_estimates[i] = alpha_map
# Compute statistics from the simulations
mean_estimate = np.mean(alpha_estimates)
std_estimate = np.std(alpha_estimates)
# Compute theoretical expectation and variance
# Since mu_alpha = 0, the theoretical expected mean of the MAP estimator is also 0
theoretical_mean = 0
# Var(y1 + y2) = Var(alpha_true + n1 + alpha_true + n2) = 4*Var(alpha_true) + 2*Var(n1 + n2)
# Var(n1 + n2) = 2*sigma2*(1 + rho)
Var_y1_plus_y2 = 4 * sigma_alpha2 + 2 * sigma2 * (1 + rho)
# Var(hat_alpha_MAP) = (sigma_alpha2 / denominator)^2 * Var(y1 + y2)
theoretical_variance = (sigma_alpha2 / denominator) ** 2 * Var_y1_plus_y2
theoretical_std = np.sqrt(theoretical_variance)
# Display results
print("Simulation Results with Random α_true:")
print(f"Prior Mean (mu_alpha): {mu_alpha}")
print(f"MAP Estimator Mean: {mean_estimate:.4f}")
print(f"Theoretical Expected Mean: {theoretical_mean:.4f}")
print(f"Bias: {mean_estimate - theoretical_mean:.4f}")
print(f"MAP Estimator Std Dev: {std_estimate:.4f}")
print(f"Theoretical Std Dev: {theoretical_std:.4f}\n")
# Visualization
# Define the number of points to plot for the subset
subset_size = 1000 # Number of points to include in the subset scatter plot
# Select a subset of the first 'subset_size' simulations for plotting
y1_subset = y1_all[:subset_size]
y2_subset = y2_all[:subset_size]
alpha_estimates_subset = alpha_estimates[:subset_size]
# Scatter plot of y1 vs y2 with color representing alpha_map
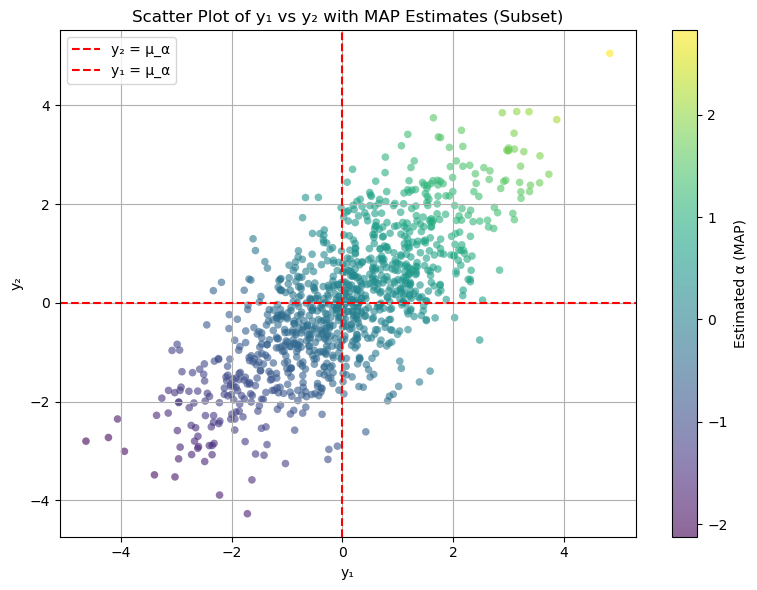
plt.figure(figsize=(8, 6))
scatter = plt.scatter(
y1_subset,
y2_subset,
c=alpha_estimates_subset,
cmap='viridis',
alpha=0.6,
marker='o',
edgecolor='none',
s=30
)
plt.colorbar(scatter, label='Estimated α (MAP)')
plt.axhline(mu_alpha, color='red', linestyle='--', linewidth=1.5, label='y₂ = μ_α')
plt.axvline(mu_alpha, color='red', linestyle='--', linewidth=1.5, label='y₁ = μ_α')
plt.title('Scatter Plot of y₁ vs y₂ with MAP Estimates (Subset)')
plt.xlabel('y₁')
plt.ylabel('y₂')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
Simulation Results with Random α_true:
Prior Mean (mu_alpha): 0
MAP Estimator Mean: -0.0042
Theoretical Expected Mean: 0.0000
Bias: -0.0042
MAP Estimator Std Dev: 0.7542
Theoretical Std Dev: 0.7559
# Visualization
# Define the number of points to plot for the subset
subset_size = 100 # Number of points to include in the subset scatter plot
# Select the first 'subset_size' simulation runs
subset_indices = np.arange(1, subset_size + 1)
subset_est_alpha = alpha_estimates[:subset_size]
subset_true_alpha = alpha_true[:subset_size] # Correctly extract the true alpha values
# Plotting the comparison
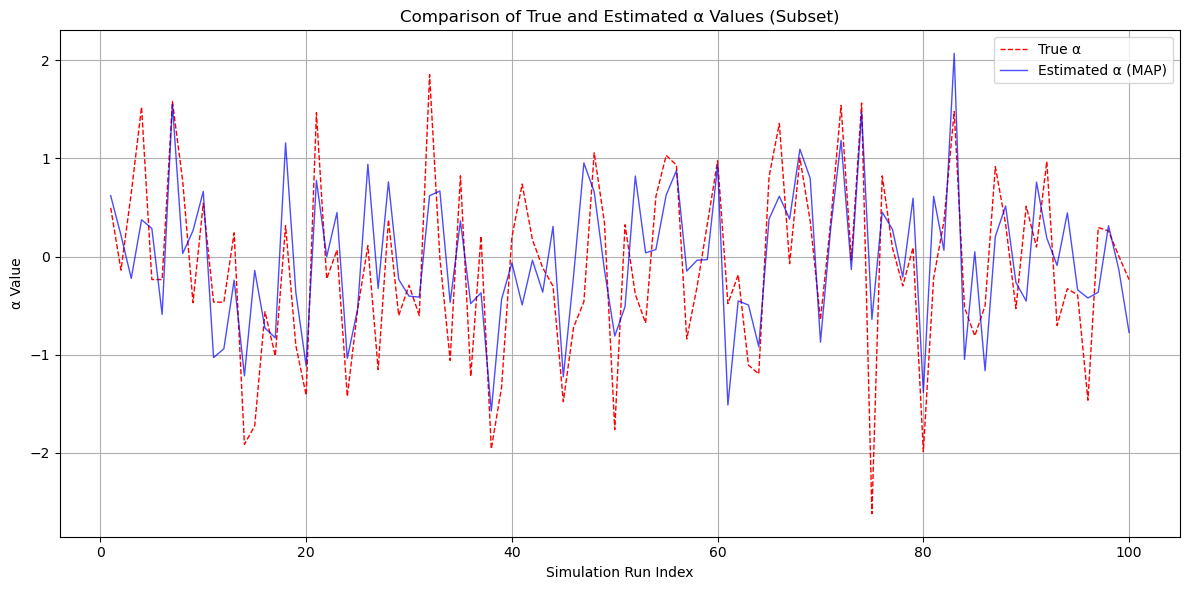
plt.figure(figsize=(12, 6))
plt.plot(subset_indices, subset_true_alpha, label='True α', color='red', linestyle='--', linewidth=1)
plt.plot(subset_indices, subset_est_alpha, label='Estimated α (MAP)', color='blue', alpha=0.7, linewidth=1)
plt.title('Comparison of True and Estimated α Values (Subset)')
plt.xlabel('Simulation Run Index')
plt.ylabel('α Value')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
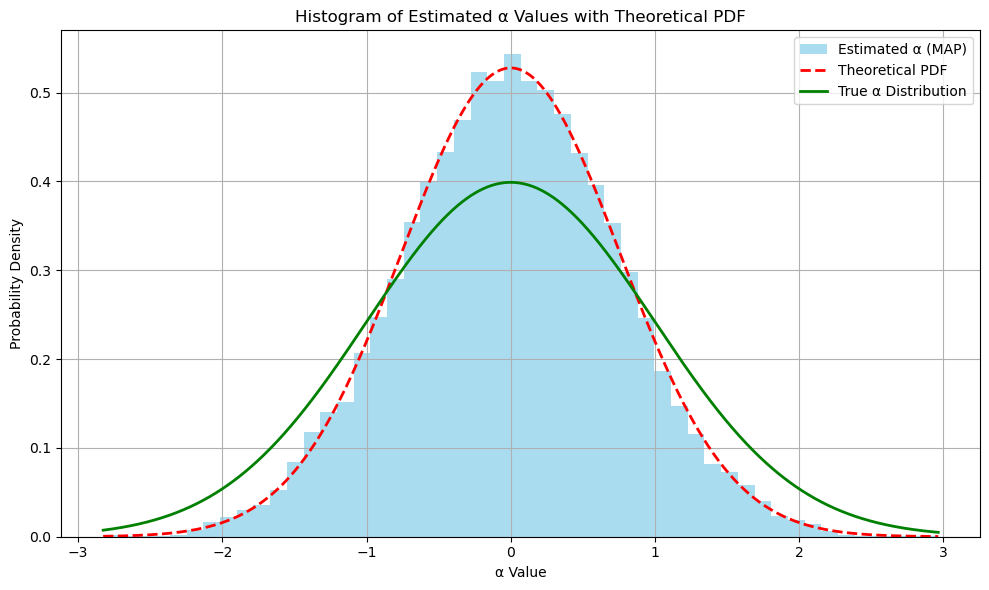
from scipy.stats import norm
# Plotting the histogram of estimated alphas
plt.figure(figsize=(10, 6))
# Histogram of alpha_estimates
count, bins, patches = plt.hist(
alpha_estimates,
bins=50,
alpha=0.7,
label='Estimated α (MAP)',
color='skyblue',
density=True # Normalize the histogram to form a probability density
)
# Overlay the theoretical PDF of the MAP estimator
# The theoretical distribution of alpha_estimates is Gaussian with:
# Mean: theoretical_mean
# Standard Deviation: theoretical_std
# From previous calculations:
# theoretical_mean = 0 (since mu_alpha = 0)
# theoretical_std = sqrt((sigma_alpha2 / denominator)^2 * (4 * sigma_alpha2 + 2 * sigma2 * (1 + rho)))
theoretical_mean = 0 # As per prior calculations
theoretical_std = np.sqrt((sigma_alpha2 / denominator) ** 2 * (4 * sigma_alpha2 + 2 * sigma2 * (1 + rho)))
# Generate points for the theoretical PDF
x = np.linspace(min(alpha_estimates), max(alpha_estimates), 1000)
pdf = norm.pdf(x, loc=theoretical_mean, scale=theoretical_std)
# Plot the theoretical PDF
plt.plot(x, pdf, 'r--', linewidth=2, label='Theoretical PDF')
# Plot the true alpha distribution
# Since alpha_true is sampled from N(mu_alpha, sigma_alpha2), overlay its PDF
true_pdf = norm.pdf(x, loc=mu_alpha, scale=np.sqrt(sigma_alpha2))
plt.plot(x, true_pdf, 'g-', linewidth=2, label='True α Distribution')
plt.title('Histogram of Estimated α Values with Theoretical PDF')
plt.xlabel('α Value')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
