Bayes Criterion

Bayes Criterion#

MOTIVATION. The question is why we need another criterion, such as Bayes criterion.

There is a fact that some decisions might be more important than others and some errors might be more costly than others.
The MAP criterion of the previous section ignores the fact.

For example, consider a hypothetical situation where you are suspected of having a fatal, yet curable, disease.

If \( H_0 \) corresponds to the hypothesis of no disease, then the following “costs” are associated with each of the four possibilities:

With probability \( P_{00} \) a correct decision is made that there is no disease. In this case, the only cost is that of the initial medical test.
With probability \( P_{01} \) an incorrect decision is made that you do not have the disease; the cost is quite high, namely, death.
With probability \( P_{10} \) and \( P_{11} \), a decision is made that you have the disease, although the decision is incorrect in the former. In both cases, the cost includes medication and perhaps further tests, surgery, or hospitalization.

Cost \( C_{ij} \), Bayes risk, \(r\), Bayes theshold#

DEFINITION. We need to the definitions of

Cost \( C_{ij} \)
Bayes risk, \(r\)
Bayes decision theshold

The Bayes criterion addresses this issue by introducing the concept of cost.

Cost \( C_{ij} \)

Let \( C_{ij} \) be the cost of deciding \( D_i \) when hypotheses \( H_j \) is correct.

Bayes risk, \(r\)

Then the average risk \( r \), called the Bayes risk, is

\[ r = [P_{00}C_{00} + P_{10}C_{10}]\pi_0 + [P_{01}C_{01} + P_{11}C_{11}]\pi_1 \]

OBJECTIVE. The question is what we need to do to optimize the Bayes criterion, to get better decision. We want to organize our decision to minimize \( r \).

We know that

\[ P_{11} = 1 - P_{01} \]

and

\[ P_{10} = 1 - P_{00} \]

From these equations, we find

\[ r = \pi_0 C_{10} + \pi_1 C_{11} - \pi_0 (C_{10} - C_{00})P_{00} + \pi_1 (C_{01} - C_{11})P_{01} \]

But

\[ P_{00} = \int_{R_0} p(y|H_0) \, dy \]

and

\[ P_{01} = \int_{R_0} p(y|H_1) \, dy \]

so

\[ r = \pi_0 C_{01} + \pi_1 C_{11} + \int_{R_0} \left\{\pi_1 (C_{01} - C_{11})p(y|H_1) - \pi_0 (C_{10} - C_{00})p(y|H_0)\right\} dy \]

Decision Making#

METHODOLOGY. The question is given the received observation, how we make a decision using the Bayes criterion, i.e., how to make decision \(D_0\) or \(D_1\) using the Bayes rule.

Since the first two terms are constant, minimizing \( r \) is equivalent to minimizing the integral in its expression.

This, in turn, is equivalent to finding the range \( R_0 \) that minimizes this integral.

Let

\[ g(y) = \pi_1 (C_{01} - C_{11}) p(y|H_1) - \pi_0 (C_{10} - C_{00}) p(y|H_0) \]

be that integrand.

The decision rule is to decide \( D_0 \) if

\[ \pi_0 (C_{10} - C_{00}) p(y|H_0) \geq \pi_1 (C_{01} - C_{11}) p(y|H_1) \]

Bayes decision threshold

\[ \tau_B \triangleq \frac{\pi_0 (C_{10} - C_{00})}{\pi_1 (C_{01} - C_{11})} \]

Recognizing this inequality as a likelihood ratio, we decide \( D_0 \) if

\[ L(y) = \frac{p(y|H_1)}{p(y|H_0)} < \frac{\pi_0 (C_{10} - C_{00})}{\pi_1 (C_{01} - C_{11})} = \tau_B \]

It follows that we decide \( D_1 \) if

\[ L(y) \geq \tau_B \]

or, in terms of our combined notation,

\[ L(y) \underset{D_0}{\overset{D_1}{\gtrless}} \tau_B \]

Thus, the Bayes test also requires using the observation \( y \) to form the likelihood ratio \( L(y) \) and comparing it with a threshold \( \tau_B \).

The design rule for the Bayes’ test is

\[\begin{split} \delta_B(y) = \begin{cases} 1, & \text{if } L(y) \geq \tau_B \\ 0, & \text{if } L(y) < \tau_B \end{cases} \end{split}\]

DISCUSSION. Compare MAP versus Bayes criterion.

If \( C_{10} - C_{00} = C_{01} - C_{11} \), then \( \tau_B = \tau_{\text{MAP}} \), i.e., it is the MAP criterion. Thus, the MAP criterion is a special case of the Bayes criterion.

Example: Antipodal Signal Detection using Bayes Criterion#

In this example [B2, Ex 4.6], we investigate the Bayes criterion by assigning costs to the decisions.

The costs are assigned (heuristically) as follows:

\( C_{00} = C_{11} = 0 \): There is no cost for making a correct decision.
\( C_{10} = 1 \): The cost of deciding \( D_1 \) when \( H_0 \) is true.
\( C_{01} = 2 \): The cost of deciding \( D_0 \) when \( H_1 \) is true.

Thus, the cost of deciding \( D_0 \) when \( H_1 \) is correct is twice as large as the converse.

To apply the Bayes criterion, we compute the Bayes decision threshold \( \tau_B \) as:

\[ \tau_B = \frac{\pi_0 (C_{10} - C_{00})}{\pi_1 (C_{01} - C_{11})} = 2 \]

Recall the concept of using \(\mathrm{func}^{-1}(\cdot)\), herein, using the log-likelihood ratio, the log-likelihood threshold \( \tau' \) is calculated as:

\[ \tau' = \ln 2 \frac{\sigma^2}{2b} \]

recall that \( s_0 = -b \) and \( s_1 = b \), and \(b>0\).

The decision rule based on this threshold is:

\[\begin{split} \delta'_B (y) = \begin{cases} D_1, & \text{if } y \geq \tau' \\ D_0, & \text{if } y < \tau' \end{cases} \end{split}\]

Thus, the decision regions are:

\( R_1 = \{ y : y \geq \ln 2 \frac{\sigma^2}{2b} \} \) (decide \( H_1 \))
\( R_0 = \{ y : y < \ln 2 \frac{\sigma^2}{2b} \} \) (decide \( H_0 \))

As a result, the probabilities are updated as follows:

\( P_{00} \approx 0.985 \)
\( P_{01} \approx 0.034 \)
\( P_{10} \approx 0.015 \)
\( P_{11} \approx 0.966 \)

Simulation#

import numpy as np

# Given parameters
b = 1
sigma2 = 0.25  # Variance
pi0 = 0.8
pi1 = 0.2

# Number of simulations
n_samples = 1000000

# Costs assigned to decisions
C00 = 0  # Cost of deciding D0 when H0 is true (correct decision, no cost)
C11 = 0  # Cost of deciding D1 when H1 is true (correct decision, no cost)
C10 = 1  # Cost of deciding D1 when H0 is true (false positive)
C01 = 2  # Cost of deciding D0 when H1 is true (false negative)

# Generating s0 and s1
s0 = -b
s1 = b

# Generating noise
noise = np.random.normal(0, np.sqrt(sigma2), n_samples)

# Simulating received y under each hypothesis
y_given_s0 = s0 + noise  # When H0 is true
y_given_s1 = s1 + noise  # When H1 is true

# Bayes decision threshold tau_B calculation
tau_B = (pi0 * (C10 - C00)) / (pi1 * (C01 - C11))

# Bayes decision threshold tau_prime using log-likelihood ratio
tau_prime_B = np.log(tau_B) * (sigma2 / (2 * b))

# Decisions based on the Bayes threshold
decisions_s0_B = y_given_s0 >= tau_prime_B  # Decide s1 if y >= threshold
decisions_s1_B = y_given_s1 >= tau_prime_B  # Decide s1 if y >= threshold

# Estimating transmitted signals (s_hat) based on decisions for Bayes criterion
s0_hat_B = np.where(decisions_s0_B, s1, s0)  # Decided s1 if decision is True, else s0 (under H0)
s1_hat_B = np.where(decisions_s1_B, s1, s0)  # Decided s1 if decision is True, else s0 (under H1)

# Calculating empirical probabilities for Bayes criterion
P00_empirical_B = np.mean(s0_hat_B == s0)  # Probability of deciding H0 when H0 is true
P01_empirical_B = np.mean(s1_hat_B == s0)  # Probability of deciding H0 when H1 is true
P10_empirical_B = np.mean(s0_hat_B == s1)  # Probability of deciding H1 when H0 is true
P11_empirical_B = np.mean(s1_hat_B == s1)  # Probability of deciding H1 when H1 is true

# Print results
print(f"Bayes, P00 (Decide H0 | H0 true) using Bayes decision threshold: {P00_empirical_B:.4f}")
print(f"Bayes, P01 (Decide H0 | H1 true) using Bayes decision threshold: {P01_empirical_B:.4f}")
print(f"Bayes, P10 (Decide H1 | H0 true) using Bayes decision threshold: {P10_empirical_B:.4f}")
print(f"Bayes, P11 (Decide H1 | H1 true) using Bayes decision threshold: {P11_empirical_B:.4f}")

Bayes, P00 (Decide H0 | H0 true) using Bayes decision threshold: 0.9850
Bayes, P01 (Decide H0 | H1 true) using Bayes decision threshold: 0.0337
Bayes, P10 (Decide H1 | H0 true) using Bayes decision threshold: 0.0150
Bayes, P11 (Decide H1 | H1 true) using Bayes decision threshold: 0.9663

Compare MAP vs. Bayes Criteria#

We consider the signal model as \( y = \sqrt{\rho} s + n \), where \( \rho \) is the transmit power of the signal \( s \) and \( n \) is the noise.

To conduct the performance comparison w.r.t. the transmit SNR, we will:

Fix the noise power (i.e., variance of \( n \)).
Vary the transmit power \( \rho \) to observe its effect on the probabilities \( P_{00} \), \( P_{01} \), \( P_{10} \), and \( P_{11} \) under both MAP and Bayes criteria.

Signal Model:

\( y = \sqrt{\rho} s + n \)
\( s \in \{s_0, s_1\} \), where \( s_0 = -b \) and \( s_1 = b \)
Noise \( n \) is Gaussian with fixed variance \( \sigma^2 \)

In the simulation, \( \rho \) represents the transmit power of the signal \( s \). Since \( \rho \) is multiplied by the signal \( s \) to form the received signal \( y = \sqrt{\rho} s + n \), it effectively scales the amplitude of the signal.

Signal-to-Noise Ratio (SNR)#

The Signal-to-Noise Ratio (SNR) is defined as the ratio of the signal power to the noise power. In this context:

\[ \text{SNR} = \frac{\text{Signal Power}}{\text{Noise Power}} \]

Given that both the signal power and the noise power are expressed in Watt, the units cancel out, making the SNR a dimensionless quantity.

It represents the relative strength of the signal compared to the noise, typically expressed in decibels (dB) when calculated as:

\[ \text{SNR (dB)} = 10 \log_{10} \left( \frac{\text{Signal Power}}{\text{Noise Power}} \right) \]

Typically, SNR is measured at the receiver side. When considering the power of the transmitted signal relative to noise, it is referred to as the transmit SNR.

# Given parameters
b = 1  # Signal amplitude
sigma2 = 0.25  # Fixed noise variance
pi0 = 0.8
pi1 = 0.2
C00 = 0
C11 = 0
C10 = 1
C01 = 2

# Define a range of SNR values in dB
snr_db_values = np.linspace(-20, 10, 20)  # SNR in dB
n_samples = 10000  # Number of samples for simulation

# Convert SNR from dB to linear scale
snr_linear_values = 10 ** (snr_db_values / 10)

# Compute the transmit power (rho) in linear scale given the noise power (sigma2)
rho_values = snr_linear_values * sigma2

# Store the results for each criterion and SNR
results_map = {"SNR (dB)": [], "P00": [], "P01": [], "P10": [], "P11": []}
results_bayes = {"SNR (dB)": [], "P00": [], "P01": [], "P10": [], "P11": []}

# Simulate for each SNR value
for snr_db, rho in zip(snr_db_values, rho_values):
    # Signal amplitudes under each hypothesis with power adjustment
    s0 = -np.sqrt(rho) * b
    s1 = np.sqrt(rho) * b
    
    # Generating noise
    noise = np.random.normal(0, np.sqrt(sigma2), n_samples)
    
    # Simulating received y under each hypothesis
    y_given_s0 = s0 + noise
    y_given_s1 = s1 + noise
    
    # MAP criterion threshold
    tau_MAP = np.log(pi0 / pi1)
    threshold_map = (sigma2 / (2 * np.sqrt(rho) * b)) * tau_MAP
    
    # Bayes decision threshold tau_B calculation
    tau_B = (pi0 * (C10 - C00)) / (pi1 * (C01 - C11))
    threshold_bayes = np.log(tau_B) * (sigma2 / (2 * np.sqrt(rho) * b))
    
    # Decisions based on the MAP threshold
    decisions_s0_map = y_given_s0 >= threshold_map
    decisions_s1_map = y_given_s1 >= threshold_map
    s0_hat_map = np.where(decisions_s0_map, b, -b)
    s1_hat_map = np.where(decisions_s1_map, b, -b)
    
    # Decisions based on the Bayes threshold
    decisions_s0_bayes = y_given_s0 >= threshold_bayes
    decisions_s1_bayes = y_given_s1 >= threshold_bayes
    s0_hat_bayes = np.where(decisions_s0_bayes, b, -b)
    s1_hat_bayes = np.where(decisions_s1_bayes, b, -b)
    
    # Calculating empirical probabilities for MAP criterion
    # P00_map = np.mean(s0_hat_map == -b)
    # P01_map = np.mean(s0_hat_map == b)
    # P10_map = np.mean(s1_hat_map == -b)
    # P11_map = np.mean(s1_hat_map == b)
    # Calculating empirical probabilities
    P00_map = np.mean(s0_hat_map == -b)  # Probability of deciding H0 when H0 is true
    P01_map = np.mean(s1_hat_map == -b)  # Probability of deciding H0 when H1 is true
    P10_map = np.mean(s0_hat_map == b)  # Probability of deciding H1 when H0 is true
    P11_map = np.mean(s1_hat_map == b)  # Probability of deciding H1 when H1 is true
    
    # Store MAP results
    results_map["SNR (dB)"].append(snr_db)
    results_map["P00"].append(P00_map)
    results_map["P01"].append(P01_map)
    results_map["P10"].append(P10_map)
    results_map["P11"].append(P11_map)
    
    # Calculating empirical probabilities for Bayes criterion
    # P00_bayes = np.mean(s0_hat_bayes == -b)
    # P01_bayes = np.mean(s0_hat_bayes == b)
    # P10_bayes = np.mean(s1_hat_bayes == -b)
    # P11_bayes = np.mean(s1_hat_bayes == b)

    # Calculating empirical probabilities for Bayes criterion
    P00_bayes = np.mean(s0_hat_bayes == -b)  # Probability of deciding H0 when H0 is true
    P01_bayes = np.mean(s1_hat_bayes == -b)  # Probability of deciding H0 when H1 is true
    P10_bayes = np.mean(s0_hat_bayes == b)  # Probability of deciding H1 when H0 is true
    P11_bayes = np.mean(s1_hat_bayes == b)  # Probability of deciding H1 when H1 is true
    
    # Store Bayes results
    results_bayes["SNR (dB)"].append(snr_db)
    results_bayes["P00"].append(P00_bayes)
    results_bayes["P01"].append(P01_bayes)
    results_bayes["P10"].append(P10_bayes)
    results_bayes["P11"].append(P11_bayes)

import matplotlib.pyplot as plt

# Plotting
plt.figure(figsize=(6, 4))

# Plot P00, P01, P10, P11 for MAP criterion
plt.plot(results_map["SNR (dB)"], results_map["P00"], label='$P_{00}$ (MAP)', marker='o',  color='tab:blue', linestyle='--')
plt.plot(results_map["SNR (dB)"], results_map["P01"], label='$P_{01}$ (MAP)', marker='*', color='tab:red', linestyle='--')
plt.plot(results_map["SNR (dB)"], results_map["P10"], label='$P_{10}$ (MAP)', marker='s', color='tab:green', linestyle='--')
plt.plot(results_map["SNR (dB)"], results_map["P11"], label='$P_{11}$ (MAP)', marker='x', color='tab:cyan', linestyle='--')

# Plot P00, P01, P10, P11 for Bayes criterion
plt.plot(results_bayes["SNR (dB)"], results_bayes["P00"], label='$P_{00}$ (Bayes)', marker='o', color='tab:blue', linestyle='-')
plt.plot(results_bayes["SNR (dB)"], results_bayes["P01"], label='$P_{01}$ (Bayes)', marker='*', color='tab:red', linestyle='-')
plt.plot(results_bayes["SNR (dB)"], results_bayes["P10"], label='$P_{10}$ (Bayes)', marker='s', color='tab:green', linestyle='-')
plt.plot(results_bayes["SNR (dB)"], results_bayes["P11"], label='$P_{11}$ (Bayes)', marker='x', color='tab:cyan', linestyle='-')

# Add labels and title
plt.xlabel('SNR (dB)')
plt.ylabel('Probability')
plt.title('Comparison of $P_{00}$, $P_{01}$, $P_{10}$, $P_{11}$ as a function of SNR (dB)')
plt.legend()
plt.grid(True)

# Show plot
plt.show()

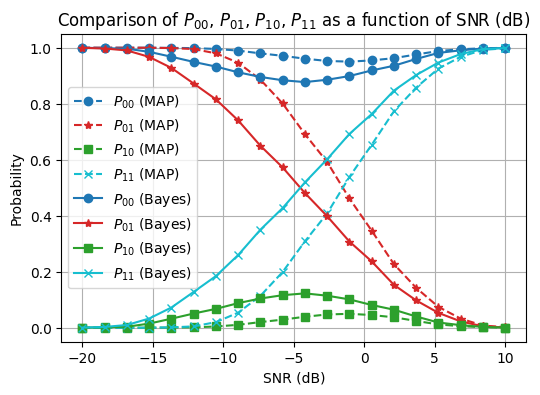
_images/390ea9825c169fc7a51e7152c6b96cac5ebf970d4000b5df1905e616b937ea07.png

DISCUSSION. This comparison may not be entirely fair because the Bayes criterion requires knowledge of both the costs associated with different types of errors and the a priori probabilities of the hypotheses.

In contrast, the MAP criterion only requires knowledge of the a priori probabilities.

This additional information for the Bayes criterion can potentially lead to more informed decision-making but also requires more detailed input, which may not always be available or accurate.