Lossy Data Compression

Data compression techniques can be broadly categorized based on the nature of the information source:

• Discrete Information Sources
  These sources produce data that take on a finite or countably infinite set of distinct values, such as text or digital signals with quantized levels.

  Compression of discrete sources can often be lossless, meaning the original data can be perfectly reconstructed from the compressed version.

• Continuous-Amplitude Information Sources
  These sources generate data with values that vary continuously over a range, such as analog audio or video signals.

  Unlike discrete sources, continuous-amplitude sources pose unique challenges for compression.

For a continuous-amplitude source, achieving perfect reconstruction—representing the source data exactly as it was before compression—requires an infinite number of bits.

This is because a general real number in base-2 (binary) representation typically requires an infinite sequence of digits to specify it precisely. For example, \(\pi\) and other irrational numbers cannot be fully captured with a finite number of bits.

Consequently, lossless compression, which guarantees perfect reconstruction, is theoretically impossible for continuous-amplitude sources. Instead, lossy compression is employed, where some information is intentionally discarded to achieve a feasible bit rate.

Two primary methods for lossy compression are:

• Scalar Quantization: Mapping each continuous value to one of a finite set of discrete levels, introducing distortion but reducing the data size.

• Vector Quantization: Extending scalar quantization by grouping multiple samples into vectors and mapping them to a finite set of representative vectors, often achieving better performance at the cost of increased complexity.

The study of lossy data compression rests on several key concepts:

• The Notion of Lossy Data Compression: The trade-off between data reduction and the acceptable level of distortion in the reconstructed signal.

• Generalization of Entropy and Mutual Information to Continuous Random Variables: Adapting these measures, originally defined for discrete systems, to continuous systems to quantify information content and dependencies.

• Rate Distortion Function: Defining the theoretical minimum bit rate required to represent a source within a specified distortion level, serving as the fundamental limit of lossy compression.

Mutual Information for Continuous Random Variables

We consider continuous random variables \(X\) and \(Y\) with a joint probability density function (PDF) \(\,p(x, y)\) and marginal PDFs \(\,p(x)\) and \(\,p(y)\).

The average mutual information, denoted by \(\,I(X; Y)\), measures the amount of information that one variable provides about the other, is defined as:

\[ \boxed{ I(X; Y) = \int_{-\infty}^{\infty} \!\!\int_{-\infty}^{\infty} p(x, y)\,\log_2 \!\Bigl(\tfrac{p(x, y)}{p(x)\,p(y)}\Bigr)\,dx\,dy. } \]

This expression measures the reduction in uncertainty about \(X\) given knowledge of \(Y\), and vice versa.

Alternatively, using conditional PDFs, it can be written as:

\[ I(X; Y) = \int_{-\infty}^{\infty} \!\!\int_{-\infty}^{\infty} p(x)\,p(y \!\mid\! x)\,\log_2 \!\Bigl(\tfrac{p(y \!\mid\! x)\,p(x)}{p(x)\,p(y)}\Bigr)\,dx\,dy, \]

where \(p(y \!\mid\! x)\) is the conditional PDF of \(Y\) given \(X = x\).

Both forms are equivalent because \(p(x, y) = p(x)\,p(y \!\mid\! x)\), and the base-2 logarithm ensures the information is measured in bits.

This definition extends the concept of mutual information from discrete to continuous random variables without alteration to its fundamental interpretation.

Entropy of Continuous Random Variables

The concept of entropy, representing the average uncertainty or information content of a random variable, does not transfer as straightforwardly from discrete to continuous random variables.

For a discrete random variable \(X\) with possible values \(\{x_1, x_2, \ldots, x_n\}\), the entropy is:

\[ H(X) = -\sum_{i=1}^{n} P(x_i)\,\log_2 P(x_i), \]

where \(n\) is finite, and \(H(X)\) is a finite, non-negative quantity.

In contrast, a continuous random variable \(X\) can take on an uncountably infinite number of values (i.e., \(n \to \infty\)), with its probability described by a PDF \(p(x)\) rather than a probability mass function.

The self-information of a specific outcome \(x\), defined as \(-\log_2 p(x)\), becomes problematic because \(p(x)\) is a density, not a discrete probability.

For a particular \(x\) in a continuous distribution, \(p(x)\,dx\) is infinitesimally small, causing \(-\log_2 p(x)\) to tend to infinity and making a direct analogy to discrete entropy infeasible.

Differential Entropy

To address this, differential entropy for a continuous random variable \(X\) is introduced:

\[ \boxed{ H(X) = - \int_{-\infty}^{\infty} p(x)\,\log p(x)\,dx. } \]

This integral combines a self-information–like term \(-\log p(x)\) with the PDF \(p(x)\) over the entire range of \(X\).

Unlike discrete entropy, differential entropy can be negative, zero, or positive, and does not represent the absolute amount of information required to specify \(X\) exactly (which is infinite).

Instead, it reflects the relative uncertainty or spread of the distribution in a continuous space. Consequently, differential entropy lacks the direct physical interpretation of self-information that discrete entropy possesses.

Average Conditional Entropy

The average conditional entropy of \(X\) given \(Y\) quantifies the remaining uncertainty about \(X\) when \(Y\) is known.

For continuous random variables with joint PDF \(p(x, y)\) and conditional PDF \(p(x\!\mid y)\), it is defined as:

\[ \boxed{ H(X\!\mid Y) = - \int_{-\infty}^{\infty} \!\!\int_{-\infty}^{\infty} p(x, y)\,\log \bigl[p(x\!\mid y)\bigr]\,dx\,dy. } \]

This expression averages the conditional self-information \(-\log p(x\!\mid y)\) over the joint distribution of \(X\) and \(Y\), representing the expected uncertainty in \(X\) given observation of \(Y\).

The average mutual information \(I(X; Y)\) can be related to differential entropy and conditional entropy through:

\[ I(X; Y) = H(X) \;-\; H(X\!\mid Y). \]

This identity states that mutual information is the reduction in uncertainty about \(X\) provided by \(Y\).

By symmetry of mutual information, we also have:

\[ I(X; Y) = H(Y) \;-\; H(Y\!\mid X), \]

where \(H(Y\!\mid X)\) is defined analogously:

\[ H(Y\!\mid X) = - \int_{-\infty}^{\infty} \!\!\int_{-\infty}^{\infty} p(x, y)\,\log \bigl[p(y\!\mid x)\bigr]\,dx\,dy. \]

These relationships link entropy, conditional entropy, and mutual information in a unified framework suitable for continuous systems.

Mixed Discrete-Continuous Random Variables

In some scenarios, one random variable is discrete while the other is continuous.

Suppose \(X\) is a discrete random variable with possible outcomes \(x_i\) (\(i = 1, 2, \ldots, n\)), each occurring with probability \(P[x_i]\), and \(Y\) is a continuous random variable with marginal PDF \(p(y)\).

If \(X\) and \(Y\) are statistically dependent, the marginal PDF of \(Y\) can be written as:

\[ p(y) = \sum_{i=1}^{n} p(y\!\mid x_i)\,P[x_i]. \]

Here, \(p(y\!\mid x_i)\) is the conditional PDF of \(Y\) given \(X = x_i\).

This formula decomposes \(p(y)\) into contributions from each possible value of \(X\), weighted by their probabilities.

The mutual information between a specific outcome \(X = x_i\) and a specific value \(Y = y\) is:

\[ I(x_i; y) = \log \frac{p(y\!\mid x_i)}{p(y)}, \]

which measures the information provided by observing \(Y = y\) about the event \(X = x_i\), expressed as the log-ratio of the conditional and marginal densities.

To obtain the average mutual information between \(X\) and \(Y\), we average over all possible outcomes of both variables:

\[ \boxed{ I(X; Y) = \sum_{i=1}^{n} \int_{-\infty}^{\infty} p(y\!\mid x_i)\,P[x_i]\,\log \!\Bigl(\tfrac{p(y\!\mid x_i)}{p(y)}\Bigr)\,dy. } \]

This formula integrates the pointwise mutual information over the continuous variable \(Y\) and sums over the discrete variable \(X\).

Example: Binary-Input Gaussian Channel

As a concrete example, let \(X\) be a discrete random variable with two equally likely outcomes, \(x_1 = A\) and \(x_2 = -A\), so \(P[x_1] = P[x_2] = \tfrac12\).

The continuous random variable \(Y\) follows a Gaussian distribution conditioned on each \(x_i\), with mean \(x_i\) and variance \(\sigma^2\):

\[ p(y\!\mid A) = \frac{1}{\sqrt{2\pi\sigma^2}}\,\exp \!\Bigl(-\tfrac{(y - A)^2}{2\sigma^2}\Bigr), \quad p(y\!\mid -A) = \frac{1}{\sqrt{2\pi\sigma^2}}\,\exp \!\Bigl(-\tfrac{(y + A)^2}{2\sigma^2}\Bigr). \]

The marginal PDF of \(Y\) is the average of these two conditional PDFs:

\[ p(y) = \tfrac12\,p(y\!\mid A) \;+\; \tfrac12\,p(y\!\mid -A). \]

Substituting the Gaussian expressions, we get:

\[ p(y) = \tfrac{1}{2\sqrt{2\pi\sigma^2}} \Bigl(\exp \!\bigl(-\tfrac{(y-A)^2}{2\sigma^2}\bigr) + \exp \!\bigl(-\tfrac{(y + A)^2}{2\sigma^2}\bigr)\Bigr). \]

The average mutual information \(I(X; Y)\) is computed using the mixed discrete-continuous formula:

\[ I(X; Y) = \sum_{i=1}^{2} \int_{-\infty}^{\infty} p(y\!\mid x_i)\,P[x_i] \,\log \!\Bigl(\tfrac{p(y\!\mid x_i)}{p(y)}\Bigr)\,dy. \]

With \(P[x_i] = \tfrac12\), this becomes:

\[ \boxed{ I(X; Y) = \tfrac12 \int_{-\infty}^{\infty} \Bigl[p(y\!\mid A)\,\log \!\bigl(\tfrac{p(y\!\mid A)}{p(y)}\bigr) \;+\; p(y\!\mid -A)\,\log \!\bigl(\tfrac{p(y\!\mid -A)}{p(y)}\bigr)\Bigr] \,dy. } \]

This integral is typically not solvable in closed form due to the logarithm of the mixture PDF. However, it represents the channel capacity of a binary-input additive white Gaussian noise (AWGN) channel, a key concept in communication theory.

The capacity depends on the signal amplitude \(A\) and noise variance \(\sigma^2\), generally increasing with the signal-to-noise ratio \(\tfrac{A^2}{\sigma^2}\).

In practice, numerical methods or approximations are employed to evaluate this integral.

Sampling then Quantizing

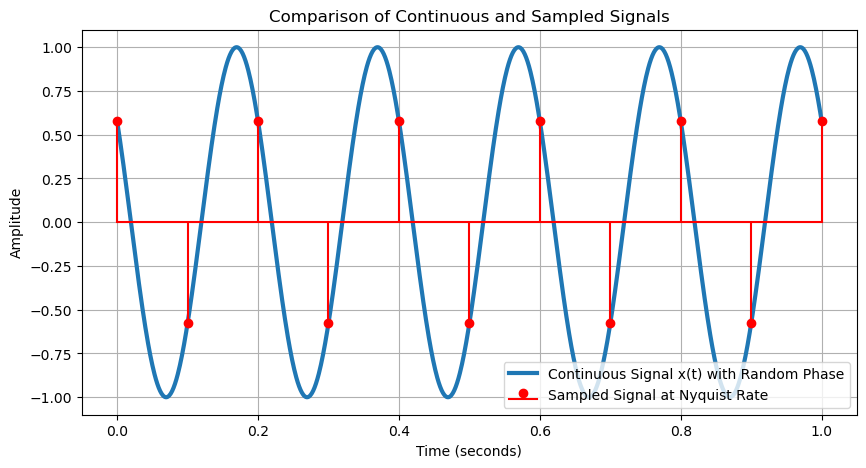
An analog source produces a message waveform \(x(t)\), which is a specific realization (or sample function) of a stochastic process \(X(t)\).

A stochastic process is a collection of random variables indexed by time, and \(x(t)\) represents one possible outcome of this process. For example, \(X(t)\) could model an audio signal with random fluctuations due to noise or variability.

When \(X(t)\) is a band-limited, stationary stochastic process, it has finite bandwidth in the range \(\,[-W, W]\), where \(W\) is the bandwidth in Hertz.

A process is stationary if its statistical properties (e.g., mean, autocorrelation) do not change over time.

Sampling

The sampling theorem states that such a process can be perfectly represented by a sequence of samples taken at the Nyquist rate, which is \(2W\) samples per second. Specifically, if \(X(t)\) is sampled at times

\[ t = \frac{k}{2W}, \quad k \in \mathbb{Z}, \]

then the continuous signal can be reconstructed from these samples using an ideal low-pass filter, provided the sampling rate is at least \(2W\).

Through this sampling, the analog output of the source is converted into an equivalent discrete-time sequence \(\{x_k\}\), where

\[ x_k = X\!\Bigl(\frac{k}{2W}\Bigr). \]

Because of the band-limited assumption, this sequence retains all the information of the original signal, making it a faithful discrete-time representation of \(X(t)\).

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the stochastic process X(t)
frequency = 5  # Frequency of the sinusoid (Hz)
amplitude = 1  # Amplitude of the sinusoid
phase = np.random.uniform(0, 2 * np.pi)  # Random phase for stochasticity
nyquist_rate = 2 * frequency  # Nyquist rate: 2 * max frequency
resolution_factor = 1  # Sampling at Nyquist rate (can increase for oversampling)
sampling_frequency = resolution_factor * nyquist_rate  # Samples per second
duration = 1  # Duration in seconds

# Time vectors
t_continuous = np.linspace(0, duration, 1000)  # Continuous time for plotting
t_samples = np.linspace(0, duration, int(duration * sampling_frequency) + 1)  # Discrete sample times

# Generate the sample function x(t) = A * sin(2πft + φ)
x_t = amplitude * np.sin(2 * np.pi * frequency * t_continuous + phase)  # Continuous signal
x_samples = amplitude * np.sin(2 * np.pi * frequency * t_samples + phase)  # Sampled signal

# Plot continuous vs. sampled signal
plt.figure(figsize=(10, 5))
plt.plot(t_continuous, x_t, label="Continuous Signal x(t) with Random Phase", linewidth=3)
plt.stem(t_samples, x_samples, linefmt='r-', markerfmt='ro', basefmt='r-', 
         label="Sampled Signal at Nyquist Rate")
plt.xlabel("Time (seconds)")
plt.ylabel("Amplitude")
plt.title("Comparison of Continuous and Sampled Signals")
plt.legend(loc='lower right')
plt.grid(True)
plt.show()

Quantization

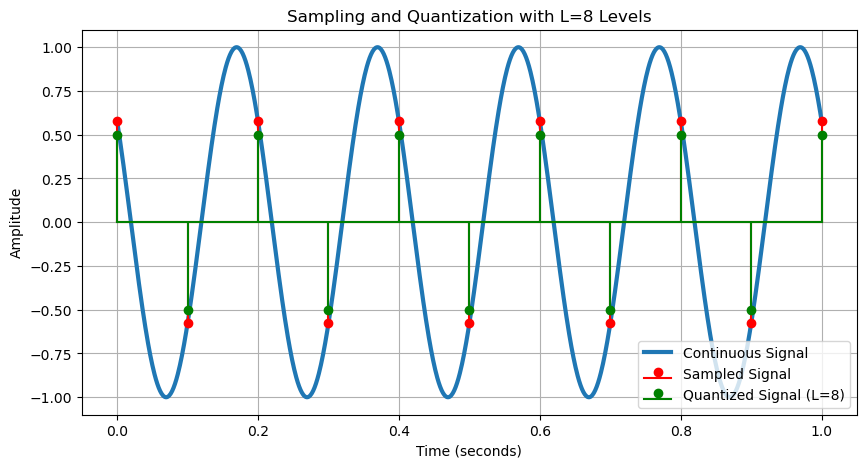
The next step is quantization, where the amplitude of each sample \(x_k\) is approximated by one of a finite set of discrete levels, producing a quantized value \(\hat{x}_k\).

Quantization reduces the precision of sample values so they can be represented digitally.

After quantization, these discrete levels are encoded into binary form. A straightforward approach is to assign each of the \(L\) levels a unique sequence of bits, converting the continuous-amplitude, discrete-time signal into a fully digital form suitable for data compression.

Bits per Sample

The number of bits per sample depends on the number of quantization levels \(L\).

If \(L\) is a power of 2 (i.e., \(L = 2^n\)), the bits per sample, denoted \(R\), is

\[ \boxed{ R = \log_2 L, } \]

since \(\log_2 L\) bits can represent \(L\) distinct levels via a fixed-length code. For instance, if \(L = 8 = 2^3\), then \(R = 3\) bits per sample.

Note that, \(R\) is measured in bit, so we must use \(\log_2\).

If \(L\) is not a power of \(2\), the number of bits must be rounded up to cover all levels:

\[ R = \lceil \log_2 L \rceil. \]

For example, if \(L = 10\), then \(\log_2 10 \approx 3.322\), so \(\lceil 3.322 \rceil = 4\) bits are required. Loosely speaking, in this case, \( R = \lceil \log_2 L \rceil = \lfloor \log_2L \rfloor + 1\).

This calculation assumes a uniform (fixed-length) encoding where each level is equally probable.

Encoding Efficiency

If the levels have different probabilities and these probabilities are known—say from the amplitude distribution of the source—variable-length encoding such as Huffman coding can assign shorter codes to more probable levels and longer codes to less probable ones.

This can reduce the average number of bits per sample below \(\log_2 L\) or \(\lceil \log_2 L \rceil\), thus improving encoding efficiency.

# Quantization parameters
L = 2**3  # Number of quantization levels (e.g., 8 levels with 3 bits)
quantization_range = 2 * amplitude  # Range from -amplitude to +amplitude
quantization_step_size = quantization_range / L  # Step size between levels

# Quantize the samples
x_quantized = np.round(x_samples / quantization_step_size) * quantization_step_size
# Clip to ensure values stay within [-amplitude, amplitude]
x_quantized = np.clip(x_quantized, -amplitude, amplitude)

# Plot continuous, sampled, and quantized signals
plt.figure(figsize=(10, 5))
plt.plot(t_continuous, x_t, label="Continuous Signal", linewidth=3)
plt.stem(t_samples, x_samples, linefmt='r-', markerfmt='ro', basefmt='r-', 
         label="Sampled Signal")
plt.stem(t_samples, x_quantized, linefmt='g-', markerfmt='go', basefmt='g-', 
         label=f"Quantized Signal (L={L})")
plt.xlabel("Time (seconds)")
plt.ylabel("Amplitude")
plt.title(f"Sampling and Quantization with L={L} Levels")
plt.legend(loc='lower right')
plt.grid(True)
plt.show()

Distortion

Quantization achieves data compression by reducing the amplitude resolution of the samples, thereby lowering the bit rate compared to an unquantized representation.

However, it introduces distortion, because the quantized values \(\hat{x}_k\) differ from the original samples \(x_k\).

The central challenge in lossy compression is to design the quantization and encoding process in a way that minimizes distortion while keeping the bit rate within acceptable limits.

Squared-Error Distortion

Quantization introduces distortion when the continuous-amplitude samples \(\{x_k\}\) are mapped to a finite set of discrete levels \(\{\hat{x}_k\}\), each represented with a fixed number of bits.

Distortion is a measure of the difference between the original sample \(x_k\) and its quantized approximation \(\hat{x}_k\), denoted \(d(x_k, \hat{x}_k)\).

A widely used distortion measure is the squared-error distortion, defined as

\[ \boxed{ d(x_k, \hat{x}_k) \;=\; (x_k - \hat{x}_k)^2. } \]

This squares the difference between the original and quantized values, placing greater emphasis on larger errors.

It is popular in signal processing for its mathematical simplicity and correspondence to the mean square error, a common fidelity metric.

For a sequence of \(n\) samples \(\vec{x}_n = (x_1, x_2, \ldots, x_n)\) and their quantized counterparts \(\vec{\hat{x}}_n = (\hat{x}_1, \hat{x}_2, \ldots, \hat{x}_n)\), the average distortion per letter is

\[ d(\vec{x}_n, \vec{\hat{x}}_n) =\; \frac{1}{n}\,\sum_{k=1}^{n} d(x_k, \hat{x}_k) =\; \frac{1}{n}\,\sum_{k=1}^{n} \bigl(x_k - \hat{x}_k\bigr)^2. \]

The Distortion \((D)\)

Since the source output \(X(t)\) is a random process, the samples \(\vec{x}_n = (X_1, X_2, \ldots, X_n)\) are random variables, and the quantized values \(\vec{\hat{x}}_n = (\hat{X}_1, \hat{X}_2, \ldots, \hat{X}_n)\) depend on the quantization process. Therefore, the distortion \(d(\vec{x}_n, \vec{\hat{x}}_n)\) is itself a random variable.

The expected distortion, denoted by \(D\), is the statistical average of this distortion over all possible realizations of the source:

\[ \boxed{ D =\; \mathbb{E}\bigl[d(\vec{x}_n, \vec{\hat{x}}_n)\bigr] =\; \mathbb{E}\!\Bigl[ \tfrac{1}{n}\!\sum_{k=1}^{n} d(X_k, \hat{X}_k) \Bigr]. } \]

By the linearity of expectation,

\[ D =\; \tfrac{1}{n}\,\sum_{k=1}^{n}\,\mathbb{E}\bigl[d(X_k, \hat{X}_k)\bigr]. \]

If the source process is stationary, then \(\mathbb{E}[d(X_k, \hat{X}_k)]\) is the same for all \(k\), and

\[ D =\; \mathbb{E}\bigl[d(X_1, \hat{X}_1)\bigr] =\; \mathbb{E}\bigl[d(X, \hat{X})\bigr]. \]

This quantity \(D\) is the long-term average distortion per sample, a key metric in evaluating the performance of a given quantization scheme for a stationary source.

# Calculate squared-error distortion for each sample
distortions = (x_samples - x_quantized) ** 2

# Calculate average distortion (empirical estimate of D)
average_distortion = np.mean(distortions)
print(f"Sampled values: {x_samples}")
print(f"Quantized values: {x_quantized}")
print(f"Average squared-error distortion per sample: {average_distortion:.6f}")

# Simulate multiple realizations to estimate expected distortion E[d(X, X̂)]
n_realizations = 100  # Number of signal realizations
distortions_all = []

for _ in range(n_realizations):
    phase = np.random.uniform(0, 2 * np.pi)  # New random phase each time
    x_samples = amplitude * np.sin(2 * np.pi * frequency * t_samples + phase)
    x_quantized = np.round(x_samples / quantization_step_size) * quantization_step_size
    x_quantized = np.clip(x_quantized, -amplitude, amplitude)
    distortions_all.append(np.mean((x_samples - x_quantized) ** 2))

expected_distortion = np.mean(distortions_all)
print(f"Expected distortion (D) over {n_realizations} realizations: {expected_distortion:.6f}")

Sampled values: [ 0.57686137 -0.57686137  0.57686137 -0.57686137  0.57686137 -0.57686137
  0.57686137 -0.57686137  0.57686137 -0.57686137  0.57686137]
Quantized values: [ 0.5 -0.5  0.5 -0.5  0.5 -0.5  0.5 -0.5  0.5 -0.5  0.5]
Average squared-error distortion per sample: 0.005908
Expected distortion (D) over 100 realizations: 0.004389

The Rate Distortion Function \(\,R(D)\)

Consider a memoryless source with a continuous-amplitude output \(X\) described by a PDF \(p(x)\), a quantized output alphabet \(\hat{X}\) (a finite set of discrete levels), and a per-letter distortion measure \(d(x, \hat{x})\).

A memoryless source implies that each sample \(X_k\) is statistically independent of the others.

The rate distortion function, denoted \(R(D)\), is the minimum rate (in bits per sample) required to represent \(X\) so that the expected distortion does not exceed \(D\).

Formally,

\[\boxed{ R(D) \;=\; \min_{\substack{p(\hat{x}\mid x) : \mathbb{E}[\,d(X, \hat{X})\,]\,\le D}} I(X;\,\hat{X}), } \]

where \(I(X;\,\hat{X})\) is the mutual information between the source output \(X\) and its quantized version \(\hat{X}\), given by

\[ I(X;\,\hat{X}) \;=\; \iint p(x, \hat{x}) \,\log_2 \!\biggl(\frac{p(x, \hat{x})}{p(x)\,p(\hat{x})}\biggr) \,dx\,d\hat{x}. \]

Since \(p(x,\hat{x}) = p(x)\,p(\hat{x}\!\mid x)\), the quantity \(p(\hat{x}\!\mid x)\) represents the conditional probability that a sample \(x\) is mapped to the discrete level \(\hat{x}\).

The minimization is performed over all possible quantization schemes (i.e., all valid choices of \(p(\hat{x}\!\mid x)\)) that satisfy the distortion constraint \(\mathbb{E}[\,d(X, \hat{X})\,]\le D\).

Intuitively, \(R(D)\) captures the trade-off between rate and distortion. Allowing larger \(D\) (i.e., more distortion) reduces \(R(D)\), whereas requiring smaller \(D\) (higher fidelity) increases \(R(D)\).

Shannon’s Third Theorem - Source Coding with a Fidelity Criterion, 1959

The function \(R(D)\) depends on two key factors:

• Source Statistics: The PDF \(p(x)\) describes how \(X\) is distributed, thus influencing how much information must be retained.

• Distortion Measure: The choice of \(d(x, \hat{x})\) (e.g., squared-error) determines how differences between \(X\) and \(\hat{X}\) are penalized.

Changes in \(p(x)\) or the distortion measure \(d(x, \hat{x})\) will alter \(R(D)\).

For many source distributions and distortion measures, \(R(D)\) does not have a closed-form expression and must be computed via numerical methods or bounds.

The significance of \(R(D)\) is encapsulated in Shannon’s Third Theorem (Source Coding with a Fidelity Criterion, 1959), which is stated as:

• If the encoding rate \(R\) exceeds \(R(D)\), the source can be compressed and reconstructed with distortion \(\,\le D\).

• If \(R < R(D)\), the distortion necessarily exceeds \(D\), no matter what coding scheme is used.

Thus, \(R(D)\) serves as a fundamental limit on the achievable rate for a given distortion level, representing the ultimate boundary of lossy compression for a memoryless source.

Rate Distortion Function for a Gaussian Source

A Gaussian source is a continuous-amplitude, memoryless source with

\[ X \sim \mathcal{N}(\mu,\,\sigma^2), \]

where \(\mu = \mathbb{E}[X]\) and \(\sigma^2\) is the variance. For the squared-error distortion

\[ d(x, \hat{x}) \;=\; (x - \hat{x})^2, \]

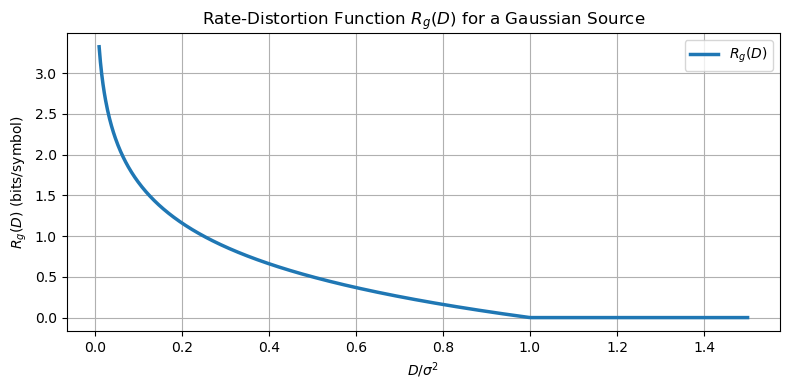
the rate distortion function is known to be:

\[\begin{split} \boxed{ R_g(D) =\; \begin{cases} \tfrac12\,\log_2 \!\bigl(\tfrac{\sigma^2}{D}\bigr), & 0 \,\le D \,\le \sigma^2,\\ [6pt] 0, & D \,>\, \sigma^2. \end{cases} } \end{split}\]

We can observe that:

• For \(0 \le D \le \sigma^2\), \(R_g(D)\) decreases as \(D\) increases, reflecting that less rate is required when higher distortion is allowed.

  The ratio \(\sigma^2 / D\) measures how the source variance compares to the allowable distortion, and the factor \(\tfrac12\) arises from properties of the Gaussian distribution.

• For \(D > \sigma^2\), we have \(R_g(D) = 0\), meaning no transmission is needed because the distortion already exceeds the natural variability of the source.

• Note that \(R_g(D)\) depends only on \(\sigma^2\), not on \(\mu\), because mean shifts do not affect squared-error distortion.

Distortion Rate Function for a Gaussian Source

When \(D \ge \sigma^2\), one can set \(\hat{X} = \mu\) (a constant reconstruction), giving

\[ \mathbb{E}[(X - \hat{X})^2] \;=\; \sigma^2, \]

thus achieving \(D = \sigma^2\) with zero rate (\(R=0\)). This matches the condition \(R_g(D) = 0\).

Reversing \(R_g(D)\) to solve for \(D\) as a function of \(R\) gives the distortion rate function:

\[\boxed{ D_g(R) =\; \sigma^2 \,2^{-2R}. } \]

Hence, the distortion decreases exponentially with rate.

The 6 dB Reduction

In decibel form,

\[ 10\,\log_{10} \!D_g(R) =\; 10\,\log_{10}\!\bigl(\sigma^2 \,2^{-2R}\bigr) =\; 10\,\log_{10}\!\bigl(\sigma^2\bigr)\;-\;10 \times 2R\,\log_{10}(2). \]

Since \(\,\log_{10}(2)\approx0.3010,\) we get \(20 \times 0.3010 \;\approx\; 6\). Thus,

\[ 10\,\log_{10} \!D_g(R) =\; -6R \;+\; 10\,\log_{10}\!\bigl(\sigma^2\bigr). \]

This reveals a 6 dB reduction in distortion for each additional bit—a classic property in Gaussian source coding.

Notes

The rate-distortion function and the distortion-rate function are inverses of each other.

Rate-Distortion Function \( R(D) \) is a function of distortion. For Gaussian source:

\[\begin{split} R(D) = \begin{cases} \tfrac12\,\log_2 \!\left(\frac{\sigma^2}{D}\right), & 0 \le D \le \sigma^2 \\ 0, & D > \sigma^2 \end{cases} \end{split}\]

Distortion-Rate Function \( D(R) \) is a function of rate. For Gaussian source:

\[ D(R) = \sigma^2\,2^{-2R} \]

They are functional inverses of each other:

• Plugging \(D(R)\) into \(R(D)\), we get back \(R\).

• Plugging \(R(D)\) into \(D(R)\), we get back \(D\).

Thus, we have

\[\begin{split} \boxed{ \begin{align*} R(D(R)) &= R \\ D(R(D)) &= D \end{align*} } \end{split}\]

They describe the same curve, just viewed from different perspectives.

Function	Input	Output	Meaning
Rate-Distortion \(R(D)\)	Distortion \(D\)	Minimum rate \(R\)	“How much rate do I need to allow distortion \(D\)?”
Distortion-Rate \(D(R)\)	Rate \(R\)	Minimum distortion \(D\)	“What distortion can I achieve with rate \(R\)?”

import numpy as np
import matplotlib.pyplot as plt

# Define the rate-distortion function R_g(D) for a Gaussian source
# with squared-error distortion: R(D) = 0.5 * log2(sigma^2 / D), valid for 0 < D <= sigma^2
def R_g(D, sigma_squared):
    # Ensure the function returns 0 outside the valid domain
    valid = (D > 0) & (D <= sigma_squared)
    R = np.zeros_like(D)
    R[valid] = 0.5 * np.log2(sigma_squared / D[valid])
    return R

# Assume sigma_squared = 1 for normalization
sigma_squared = 1.0

# Create a range of D values from 0.01 to 1.5 * sigma_squared
D_values = np.linspace(0.01, 1.5 * sigma_squared, 1000)
R_values = R_g(D_values, sigma_squared)

# Plot the rate-distortion function
plt.figure(figsize=(8, 4))
plt.plot(D_values / sigma_squared, R_values, linewidth=2.5, label=r'$R_g(D)$')
plt.xlabel(r'$D / \sigma^2$')
plt.ylabel(r'$R_g(D)$ (bits/symbol)')
plt.title('Rate-Distortion Function $R_g(D)$ for a Gaussian Source')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()

Bounds on Rate Distortion for Non-Gaussian Sources

For a general memoryless, continuous-amplitude source under the squared-error criterion, closed-form expressions for \(R(D)\) are rarely available. However, there exist some bounds.

Upper Bound

If a source has zero mean and variance \(\sigma^2\), an upper bound is

\[ R(D) \;\le\; \tfrac12 \,\log_2\!\Bigl(\tfrac{\sigma^2}{D}\Bigr), \quad 0 \,\le D \,\le \sigma^2, \]

which equals the Gaussian rate distortion function \(R_g(D)\). This indicates the Gaussian source is the worst-case among all sources with variance \(\sigma^2\), requiring the highest rate for any given distortion.

Shannon Lower Bound and Differential Entropy

A lower bound, sometimes called the Shannon lower bound, is

\[\boxed{ R^*(D) = H(X) \;-\; \tfrac12\,\log_2\!\bigl(2\pi e\,D\bigr), } \]

where

\[ H(X) = \;-\!\int p(x)\,\log_2 p(x)\,\mathrm{d}x \]

is the differential entropy of the source.

The associated distortion rate function is

\[ \boxed{ D^*(R) = \tfrac{1}{2\pi e}\;2^{\,2\,[\,H(X)\,-\,R\,]}. } \]

Hence, for any continuous source,

\[ \boxed{ R^*(D) \;\le\; R(D) \;\le\; R_g(D), \quad\text{and}\quad D^*(R) \;\le\; D(R) \;\le\; D_g(R). } \]

For a Gaussian source, the differential entropy is
$\( H_g(X) =\; \tfrac12\,\log_2\!\bigl(2\pi e\,\sigma^2\bigr), \)$

and substituting this into \(R^*(D)\) recovers \(R_g(D)\).

Thus, the bounds meet exactly in the Gaussian case.

Moreover, \(H(X)\le H_g(X)\), with equality if and only if \(X\) is Gaussian, underscoring the Gaussian source as the extremal case.

Rate Distortion for a Binary Source with Hamming Distortion

Consider a binary source with \(X \in \{0, 1\}\) such that

\[ P[X = 1] = p, \quad P[X = 0] = 1-p, \]

and binary entropy

\[ H_b(p) =\; -\,p\,\log_2(p)\;-\;(1 - p)\,\log_2(1 - p). \]

For lossless compression, we require \(R \ge H_b(p)\). If \(R < H_b(p)\), some lossy compression becomes necessary, causing errors.

The Hamming distortion is defined as

\[\begin{split} d(x, \hat{x}) =\; \begin{cases} 1, & x \neq \hat{x}, \\ 0, & x = \hat{x}. \end{cases} \end{split}\]

Hence, the expected distortion is the error probability,

\[ \mathbb{E}[\,d(X, \hat{X})\,] =\; P[X \neq \hat{X}] =\; P_e. \]

The rate distortion function for this binary source under Hamming distortion is:

\[\begin{split} \boxed{ R(D) =\; \begin{cases} H_b(p)\;-\;H_b(D), & 0 < D < \min\{p,\;1 - p\}, \\ 0, & \text{otherwise}. \end{cases} } \end{split}\]

As \(D \to 0\), \(H_b(D) \to 0\), so \(R(D) \to H_b(p)\), matching the lossless limit.

Example: Binary Symmetric Source

For a binary symmetric source where \(p = 0.5\), we have \(H_b(0.5) = 1\).

Compressing at a rate \(R = 0.75 < 1\) necessitates lossy coding.

Under Hamming distortion, \(D = P_e\), so

\[ R(P_e) =\; 1 \;-\; H_b(P_e). \]

Setting \(R(P_e) = 0.75\) gives

\[ 1 \;-\; H_b(P_e) =\; 0.75 \;\;\Longrightarrow\;\; H_b(P_e) =\; 0.25. \]

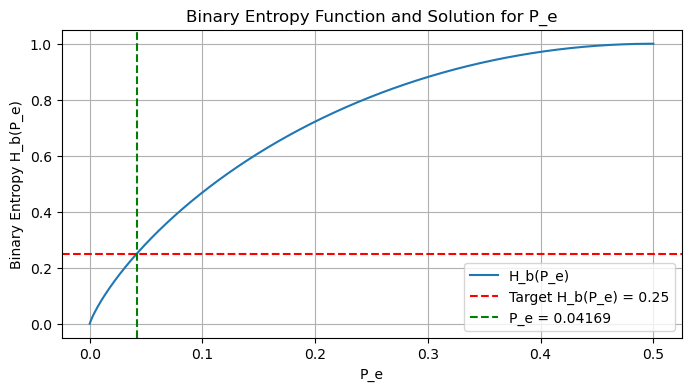
We solve \(H_b(P_e) = 0.25\) numerically:

\[ -P_e \,\log_2(P_e) \;-\; \bigl(1 - P_e\bigr)\,\log_2\bigl(1 - P_e\bigr) =\; 0.25. \]

The solution yields \(P_e \approx 0.04169\), which is the minimum error probability attainable at this rate.

Example: Binary Symmetric Source with Lossy Compression

Consider a binary symmetric source (BSS) that generates symbols
\( X \in \{0, 1\} \),
where each symbol is equally likely:
\( P(X = 0) = P(X = 1) = p = 0.5 \).

The entropy of this source, measured in bits, is given by the binary entropy function \( H_b(p) \):

\[ H_b(p) = -p \log_2(p) - (1 - p) \log_2(1 - p) \]

For \( p = 0.5 \):

\[ H_b(0.5) = -0.5 \log_2(0.5) - 0.5 \log_2(0.5) = 0.5 + 0.5 = 1 \text{ bit per symbol} \]

This entropy, \( H_b(0.5) = 1 \), represents the minimum rate required for error-free compression of the source, according to Shannon’s source coding theorem.

Now, suppose we aim to compress this source at a rate
\( R = 0.75 \) bits per symbol,
which is less than the source entropy:
\( R = 0.75 < H_b(0.5) = 1 \).

Since the rate is below the entropy, error-free compression is not possible. Therefore, we must use lossy compression, accepting some distortion in the reconstructed output.

Distortion Measure: Hamming Distortion

We use the Hamming distortion to quantify the error between the source output \( X \) and the reconstructed output \( \hat{X} \). For a binary source, Hamming distortion is defined as:

\[\begin{split} \boxed{ d(X, \hat{X}) = \begin{cases} 0 & \text{if } X = \hat{X}, \\ 1 & \text{if } X \neq \hat{X} \end{cases} } \end{split}\]

The expected distortion, denoted \( D \), is the probability of reconstruction error, i.e.,

\[ D = \mathbb{E}[d(X, \hat{X})] = P(X \neq \hat{X}) = P_e \]

Thus, in this context, the distortion \( D \) is equivalent to the error probability \( P_e \).

Rate-Distortion Function for a Binary Symmetric Source

For a BSS with Hamming distortion, the rate-distortion function \( R(D) \) gives the minimum rate required to achieve a distortion no greater than \( D \):

\[ R(D) = H_b(p) - H_b(D), \quad \text{for } 0 \leq D \leq p \]

Here, \( p = 0.5 \), and since \( D = P_e \), we get:

\[ R(P_e) = H_b(0.5) - H_b(P_e) = 1 - H_b(P_e) \]

The function \( H_b(P_e) \) is the binary entropy of the error probability:

\[ H_b(P_e) = -P_e \log_2(P_e) - (1 - P_e) \log_2(1 - P_e) \]

The Minimum Error Probability

We are given a compression rate:

\[ R = 0.75 \]

Using the rate-distortion function:

\[ R(P_e) = 1 - H_b(P_e) = 0.75 \Rightarrow H_b(P_e) = 1 - 0.75 = 0.25 \]

We must now solve for \( P_e \) such that:

\[ H_b(P_e) = 0.25 \]

Numerical Approximation of \( P_e \)

The function \( H_b(x) \) is symmetric about \( x = 0.5 \), where it reaches its maximum value of 1. It decreases toward 0 as \( x \to 0 \) or \( x \to 1 \).

Since \( P_e \) represents an error probability, we restrict \( 0 \leq P_e \leq 0.5 \). We seek a value in this range such that \( H_b(P_e) = 0.25 \).

Try \( P_e = 0.1 \):

\[ \log_2(0.1) \approx -3.3219,\quad \log_2(0.9) \approx -0.152 \]

\[ H_b(0.1) = -0.1(-3.3219) - 0.9(-0.152) \approx 0.33219 + 0.1368 = 0.46899 \]

Too high. Try \( P_e = 0.05 \):

\[ \log_2(0.05) \approx -4.3219,\quad \log_2(0.95) \approx -0.074 \]

\[ H_b(0.05) = -0.05(-4.3219) - 0.95(-0.074) \approx 0.2161 + 0.0703 = 0.2864 \]

Still too high. Try \( P_e = 0.04 \):

\[ \log_2(0.04) \approx -4.6439,\quad \log_2(0.96) \approx -0.059 \]

\[ H_b(0.04) = -0.04(-4.6439) - 0.96(-0.059) \approx 0.1858 + 0.0566 = 0.2424 \]

Now, \( H_b(0.04) \approx 0.2424 \), slightly below 0.25.

Since \( H_b(0.04) \approx 0.2424 \) and \( H_b(0.05) \approx 0.2864 \), the desired value of \( P_e \) lies between 0.04 and 0.05.

Using more accurate numerical methods (e.g., interpolation or a numerical solver), we find:

\[ P_e \approx 0.04169 \]

Confirming:

\[ H_b(0.04169) \approx 0.25 \]

We can see that

\[ P_e \approx 0.04169 \]

is the minimum error probability achievable when compressing the binary symmetric source at rate
\( R = 0.75 \) bits per symbol
under Hamming distortion.

This means that, on average, approximately 4.169% of the reconstructed symbols will differ from the original source symbols.

This is the best possible performance at this rate, assuming an ideal system with unlimited complexity and delay, as typical in information-theoretic bounds.

Simulation

We have

• Source: Binary symmetric with \( p = 0.5 \); entropy \( H_b(0.5) = 1 \)

• Rate: \( R = 0.75 < 1 \) → lossy compression required

• Distortion: Hamming distortion; \( D = P_e \)

• Rate-Distortion Function: \( R(P_e) = 1 - H_b(P_e) \)

• Solve:

  \[ 1 - H_b(P_e) = 0.75 \Rightarrow H_b(P_e) = 0.25 \Rightarrow P_e \approx 0.04169 \]

The minimum error probability at rate \( R = 0.75 \) is

\[\boxed{ P_e \approx 0.04169 } \]

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve

# Step 1: Define the binary entropy function
def binary_entropy(p):
    # Handle edge cases to avoid log(0)
    p = np.clip(p, 1e-10, 1 - 1e-10)
    return -p * np.log2(p) - (1 - p) * np.log2(1 - p)

# Step 2: Numerically solve for P_e where H_b(P_e) = 0.25
def solve_pe(target_entropy):
    # Define the equation H_b(P_e) - 0.25 = 0
    def equation(p):
        return binary_entropy(p) - target_entropy
    
    # Use fsolve to find P_e, starting with an initial guess
    pe_initial_guess = 0.04
    pe_solution = fsolve(equation, pe_initial_guess)[0]
    return pe_solution

# Step 3: Simulate the binary symmetric source and lossy compression
def simulate_bss_compression(num_symbols, target_rate, theoretical_pe):
    # Generate binary symmetric source symbols (0 or 1 with p = 0.5)
    source = np.random.choice([0, 1], size=num_symbols, p=[0.5, 0.5])
    
    # Simulate lossy compression:
    # To achieve R = 0.75 bits per symbol, we introduce errors.
    # A simple (not optimal) way to simulate this is to flip bits with probability P_e.
    # In practice, this would be done with a proper rate-distortion code,
    # but here we approximate by directly introducing errors.
    reconstructed = source.copy()
    flip_indices = np.random.rand(num_symbols) < theoretical_pe
    reconstructed[flip_indices] = 1 - reconstructed[flip_indices]  # Flip 0 to 1 or 1 to 0
    
    # Calculate empirical P_e
    errors = np.sum(source != reconstructed)
    empirical_pe = errors / num_symbols
    
    return source, reconstructed, empirical_pe

# Step 4: Run the simulation and compare results
def main():
    # Parameters
    num_symbols = 1000000  # Number of symbols to simulate
    target_rate = 0.75
    target_entropy = 1 - target_rate  # H_b(P_e) = 1 - R = 0.25
    
    # Solve for theoretical P_e
    theoretical_pe = solve_pe(target_entropy)
    print(f"Theoretical P_e (numerical solution): {theoretical_pe:.5f}")
    print(f"Binary entropy H_b({theoretical_pe:.5f}) = {binary_entropy(theoretical_pe):.5f}")
    
    # Run the simulation
    source, reconstructed, empirical_pe = simulate_bss_compression(num_symbols, target_rate, theoretical_pe)
    print(f"Empirical P_e from simulation: {empirical_pe:.5f}")
    
    # Plot the binary entropy function and the solution
    pe_values = np.linspace(0, 0.5, 1000)
    entropy_values = binary_entropy(pe_values)
    
    plt.figure(figsize=(8, 4))
    plt.plot(pe_values, entropy_values, label='H_b(P_e)')
    plt.axhline(y=target_entropy, color='r', linestyle='--', label=f'Target H_b(P_e) = {target_entropy}')
    plt.axvline(x=theoretical_pe, color='g', linestyle='--', label=f'P_e = {theoretical_pe:.5f}')
    plt.xlabel('P_e')
    plt.ylabel('Binary Entropy H_b(P_e)')
    plt.title('Binary Entropy Function and Solution for P_e')
    plt.legend()
    plt.grid(True)
    plt.show()

if __name__ == "__main__":
    main()

Theoretical P_e (numerical solution): 0.04169
Binary entropy H_b(0.04169) = 0.25000
Empirical P_e from simulation: 0.04142