Phase Estimation in AWGN

In this section, the phase \( \theta \) in the measured signal \( y_i = a \sin(\beta i + \theta) + n_i \), \( 1 \leq i \leq k \), is to be estimated.

Conditional PDF

For convenience, the conditional pdf of the received signal (for non-coherent detection in AWGN) is

\[ p(\vec{y}|a, \theta) = \kappa_1 \exp \left( \frac{a y_I}{\sigma^2} \cos \theta + \frac{a y_Q}{\sigma^2} \sin \theta - \frac{a^2 k}{4 \sigma^2} \right) \]

where \( \kappa_1 \) is a constant independent of both \( a \) and \( \theta \).

An ML estimate for the phase can be obtained by computing the maximum of \( \ln p(\vec{y}|a, \theta) \), i.e.,

\[ \frac{\partial}{\partial \theta} \ln p(\vec{y}|a, \theta) = -\frac{a y_I}{\sigma^2} \sin \hat{\theta} + \frac{a y_Q}{\sigma^2} \cos \hat{\theta} = 0 \]

Ignoring the meaningless solution \( a = 0 \), this equation can be solved for the ML estimate \( \hat{\theta}_{ML} \), yielding

\[ \boxed{ \hat{\theta}_{ML} = \tan^{-1} \frac{y_Q}{y_I}, \quad -\pi \leq \hat{\theta}_{ML} \leq \pi } \]

where

\[\begin{split} \begin{align*} y_I &= \sum_{i=1}^k y_i \sin \beta i \\ y_Q &= \sum_{i=1}^k y_i \cos \beta i \end{align*} \end{split}\]

MAP Estimation

A MAP estimate for the phase can be computed by utilizing Bayes’ rule identity

\[ p(a, \theta|\vec{y}) = \frac{p(\vec{y}|a, \theta) p(a, \theta)}{p(\vec{y})} \]

Assuming that the amplitude and phase are independent, this equation becomes

\[ p(a, \theta | \vec{y}) = \frac{p(\vec{y} | a, \theta) p(a) p(\theta)}{p(\vec{y})} \]

Substituting the conditional pdf \( p(\vec{y} | a, \theta) \) obtained, i.e.:

\[ p(\vec{y}|a, \theta) = \kappa_1 \exp\left(\frac{a}{\sigma^2} y_I \cos \theta + \frac{a}{\sigma^2} y_Q \sin \theta - \frac{a^2 k}{4\sigma^2}\right) \]

into this equation results in

\[ p(a, \theta | \vec{y}) = \kappa_a p(\theta) \exp \left( \frac{a y_I}{\sigma^2} \cos \theta + \frac{a y_Q}{\sigma^2} \sin \theta \right) \]

where

\[ \kappa_a \triangleq \kappa_1 \exp(-a^2 k / 4 \sigma^2) p(a) / p(\vec{y}) \]

is a constant independent of \( \theta \).

For any specific a priori pdf \( p(\theta) \), the maximum of \( p(a, \theta | \vec{y}) \) may have to be determined numerically.

Example

In this example [B2, Ex 11.6], if we assume that the phase is uniformly distributed in the interval \( (-\pi, \pi) \), a MAP estimate of \( \theta \) can be obtained by differentiating \( p(a, \theta | \vec{y}) \) with respect to \( \theta \), i.e.,

\[ \frac{\partial}{\partial \theta} p(a, \theta | \vec{y}) = \frac{\kappa_a}{2\pi} \exp \left( \frac{a y_I}{\sigma^2} \cos \theta + \frac{a y_Q}{\sigma^2} \sin \theta \right) \left[ -\frac{a}{\sigma^2} y_I \sin \theta + \frac{a}{\sigma^2} y_Q \cos \theta \right] \]

Setting the previous equation to zero and solving for \( \hat{\theta}_{MAP} \) yields

\[\boxed{ \hat{\theta}_{MAP} = \tan^{-1} \frac{y_Q}{y_I}, \quad -\pi \leq \hat{\theta}_{MAP} \leq \pi } \]

Phase-Locked Loop (PLL)

Often it is not possible to obtain an explicit representation of a parameter estimate.

Nonetheless, the equations that lead to a MAP or ML estimate can usually be implemented.

To illustrate this concept,

recall that

\[\begin{split} \begin{align*} y_I &= \sum_{i=1}^k y_i \sin \beta i \\ y_Q &= \sum_{i=1}^k y_i \cos \beta i \end{align*} \end{split}\]

The equation

\[ \frac{\partial}{\partial \theta} \ln p(\vec{y}|a, \theta) = -\frac{a y_I}{\sigma^2} \sin \hat{\theta} + \frac{a y_Q}{\sigma^2} \cos \hat{\theta} = 0 \]

becomes

\[ -\sum_{i=1}^{k} y_i \sin \beta i \sin \hat{\theta}_{ML} + \sum_{i=1}^{k} y_i \cos \beta i \cos \hat{\theta}_{ML} = 0 \]

or

\[ \sum_{i=1}^{k} y_i \cos(\beta i + \hat{\theta}_{ML}) = 0 \]

This equation can be implemented in approximate form using the block diagram shown in Figure 11.11, where \(\tilde{\theta}_{ML}\) is an approximation of \(\hat{\theta}_{ML}\).

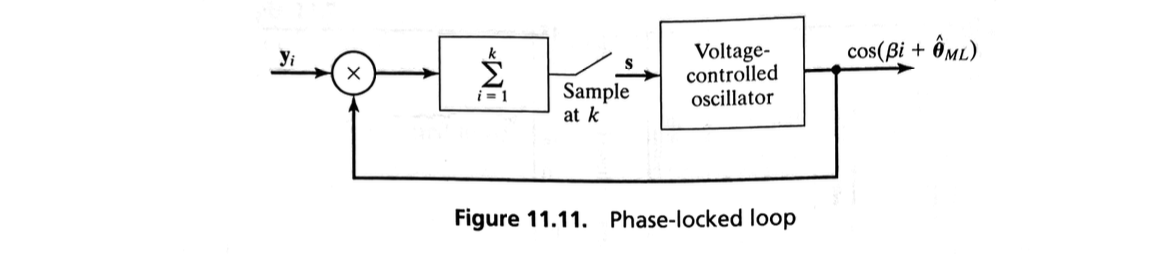
The block diagram shown in this figure is known as a phase-locked loop (PLL).

Matlab Example

• Sinusoidal Measurement (PLL)