Example: Detection with Real Additive Gaussian Noise#
In this example, based on [B2, Ex. 5.1], we consider a detection problem where we use these multiple (discrete) samples to decide between the two hypotheses \( H_0 \) and \( H_1 \).
We assume that we have \( k \) real samples or measurements \( \mathbf{y}_1, \mathbf{y}_2, \ldots, \mathbf{y}_k \).
Furthermore, we have \( 2k \) values or signal samples; \( s_{0j} \), \( j = 1, \ldots, k \), are associated with hypothesis \( H_0 \) and \( s_{1j} \), \( j = 1, \ldots, k \), with hypothesis \( H_1 \), respectively.
The real measurements can then be written as
where \( \mathbf{n}_j \) is the random variable corresponding to the \( j \)-th noise sample.
Consider the above model, where, under hypothesis \( H_0 \), the signal samples form a column vector \( \vec{s}_0 = [s_{01}, \ldots, s_{0k}]^T \) and under \( H_1 \) they form the column vector \( \vec{s}_1 = [s_{11}, \ldots, s_{1k}]^T \).
The noise samples are real zero-mean Gaussian random variables characterized by their \( k \times k \) cross-correlation matrix \( R_n \), i.e., the \( i \)-th row and \( j \)-th column of \( R_n \) is \( E\{n_i n_j\} \).
Step 1: Finding the Likelihood Ratio#
First, we derive the probability density functions \( p_0(\vec{y}) \) and \( p_1(\vec{y}) \) under hypotheses \( H_0 \) and \( H_1 \), respectively.
We will then derive the vector likelihood ratio \( L(\vec{y}) \) and simplify it using the properties of the covariance matrix \( R_n \).
Deriving the Probability Density Functions (PDFs)#
Measurements: We have a \( k \)-dimensional real-valued measurement vector:
Hypotheses:
\( H_0 \): The measurement vector is modeled as:
\[ \vec{y} = \vec{s}_0 + \vec{n} \]\( H_1 \): The measurement vector is modeled as:
\[ \vec{y} = \vec{s}_1 + \vec{n} \]
Noise: The noise vector \( \vec{n} \) is a \( k \)-dimensional Gaussian random vector with zero mean and covariance matrix \( R_n \):
Premilinary. The Multivariate Gaussian Distribution
The multivariate Gaussian distribution \( \mathcal{N}(\vec{\mu}, \Sigma) \) in \( \mathbb{R}^k \) describes a vector of \( k \) correlated Gaussian random variables.
Its PDF is given by:
where:
\( \vec{\mu} \) is the mean vector.
\( \Sigma \) is the covariance matrix.
\( |\Sigma| \) is the determinant of \( \Sigma \).
The PDF encapsulates both the spread (via \( \Sigma \)) and the central tendency (via \( \vec{\mu} \)) of the distribution.
Probability Density Function under \( H_0 \) (\( p_0(\vec{y}) \))
Under hypothesis \( H_0 \), the measurement vector is:
Since \( \vec{n} \) is Gaussian with mean \( \vec{0} \) and covariance \( R_n \), it follows that \( \vec{y} \) is also Gaussian with mean \( \vec{s}_0 \) and covariance \( R_n \):
The probability density function (PDF) of a multivariate Gaussian distribution \( \mathcal{N}(\vec{\mu}, \Sigma) \) in \( \mathbb{R}^k \) is given by:
Applying this formula to \( H_0 \):
Probability Density Function under \( H_1 \) (\( p_1(\vec{y}) \))
Similarly, under hypothesis \( H_1 \), the measurement vector is:
Thus, \( \vec{y} \) is Gaussian with mean \( \vec{s}_1 \) and covariance \( R_n \):
The PDF under \( H_1 \) is:
Formulating the Vector Likelihood Ratio \( L(\vec{y}) \)#
The likelihood ratio \( L(\vec{y}) \) is:
Substituting the expressions for \( p_1(\vec{y}) \) and \( p_0(\vec{y}) \):
Simplifying the ratio of exponentials:
Let’s denote the exponent by \( \text{exponent} \):
Expanding the Quadratic Forms
Expanding each quadratic form in \( \text{exponent} \):
Substituting these back into \( \text{exponent} \):
Thus, the likelihood ratio becomes:
Simpligying \(L(\vec{y})\) Utilizing the Symmetry of \( R_n^{-1} \)
Given that \( R_n \) is a Toeplitz matrix, it possesses specific structural properties:
Toeplitz Property: A Toeplitz matrix is constant along its diagonals. This property, however, isn’t directly relevant to symmetry but plays a role in the structure of the inverse.
Symmetry: More importantly, \( R_n \) being Toeplitz and a covariance matrix implies that it is symmetric, i.e., \( R_n^T = R_n \). Consequently, its inverse \( R_n^{-1} \) is also symmetric:
\[ (R_n^{-1})^T = R_n^{-1} \]
This symmetry is crucial because it allows us to interchange vectors in quadratic forms without changing the value.
Specifically, for any vectors \( \vec{a} \) and \( \vec{b} \):
Applying this to our case:
Simplifying the Likelihood Ratio
Using the symmetry property, we can rewrite the likelihood ratio expression:
Thus, we have the simplified expression:
Log-Likelihood Ratio:
Taking the natural logarithm of \( L(\vec{y}) \), we obtain the log-likelihood ratio \( \ell(\vec{y}) \):
Discussion. Significance of the Covariance Matrix \( R_n \)
The covariance matrix \( R_n \) encapsulates the statistical properties of the noise affecting the measurements.
Its properties significantly influence the form of the likelihood ratio and, consequently, the performance of the detection algorithm:
Diagonal \( R_n \): If \( R_n \) is diagonal, it implies that the noise components across different measurements are uncorrelated. This simplifies computations as \( R_n^{-1} \) is also diagonal.
Toeplitz \( R_n \): A Toeplitz covariance matrix indicates that the noise has a specific structure, often arising in signal processing applications where noise exhibits stationarity.
While \( R_n^{-1} \) retains the Toeplitz structure, the primary benefit is in computational efficiency and exploiting the matrix structure for optimized algorithms.
Leveraging the structure of \( R_n \) can lead to more efficient implementations, especially for high-dimensional data where matrix operations can be computationally intensive.
Decision-Making Process#
The decision-making process in this detection problem, focusing on how the log-likelihood ratio \( \ell(\vec{y}) \) is used to formulate a practical decision rule.
Short answer: it simplifies to comparing a weighted sum of the measurements \( \vec{y} \) against a threshold \( \eta_0 \).
Decision Making Using the Likelihood Ratio
A decision rule is established based on \( L(\vec{y}) \):
If \( L(\vec{y}) > \eta \): Decide in favor of \( H_1 \).
If \( L(\vec{y}) \leq \eta \): Decide in favor of \( H_0 \).
Here, \( \eta \) is a predetermined threshold that balances.
If using LLR, we have
The choice of \( \eta \) can be optimized based on specific performance criteria, such as minimizing the probability of error or maximizing the detection probability for a given false alarm rate.
Step 2: Determining the Decision Threshold#
Formulating the Decision Rule#
We have the log-likelihood ratio:
In hypothesis testing, decision rules determine which hypothesis to accept based on the observed data or statistic.
Here, we compare the statistic, i.e., log-likelihood ratio \( \ell(\vec{y}) \), against a predefined threshold \( \eta_{L} \):
Here:
\( D_0 \): Decision in favor of \( H_0 \) (null hypothesis).
\( D_1 \): Decision in favor of \( H_1 \) (alternative hypothesis).
Finding the Decision Threshold#
Analyzing the Components of \( \ell(\vec{y}) \)
We dissect the expression for \( \ell(\vec{y}) \):
Here, where have
Linear Term: Weighted Sum of Measurements:
This term is a linear combination of the measurement vector \( \vec{y} \).
Weights: The weights are given by \( (\vec{s}_1 - \vec{s}_0)^T R_n^{-1} \), which depend on the signal differences between the two hypotheses and the noise covariance matrix \( R_n \).
Interpretation: It represents how the measurements align with the direction that favors \( H_1 \) over \( H_0 \).
Constant Terms: Shift in Threshold
These terms do not depend on the measurements \( \vec{y} \).
They are constants for the decision rule, determined solely by the known signal vectors \( \vec{s}_0 \) and \( \vec{s}_1 \), and the noise covariance \( R_n \).
Role: They effectively shift the threshold \( \eta_{L} \) in the decision rule.
Simplifying the Decision Rule
Given that the second and third terms in \( \ell(\vec{y}) \) are constants, we can incorporate them into the threshold \( \eta_{L} \) as follows:
Original Decision Rule:
Isolating the Linear Term:
Defining the New Threshold \( \eta_0 \):
Let:
Rearranging the inequality:
Thus, the decision rule simplifies to:
where \( \eta_0 \) is a new threshold that incorporates both the original threshold \( \eta_{L} \) and the constant terms from \( \ell(\vec{y}) \).
Decision Rule#
Test Statistic
\( T(\vec{y}) \) is a weighted sum of the measurements \( \vec{y} \).
Decision Criterion:
If \( T(\vec{y}) > \eta_0 \): Decide \( D_1 \) (favor \( H_1 \)).
If \( T(\vec{y}) \leq \eta_0 \): Decide \( D_0 \) (favor \( H_0 \)).
We can adjust the threshold based on the known signal vectors and noise characteristics.
Discussion.
In this problem, the decision threshold (e.g., \( \eta_L \), \( \eta_0 \), or \( \eta_{NP} \)) is a scalar.
In binary hypothesis testing, the decision rule generally compares a scalar statistic (e.g., the log-likelihood ratio \( \ell(\vec{y}) \)) against a scalar threshold \( \eta \).
Specifically, we compare \( \ell(\vec{y}) \) or a linear combination of measurements \( (\vec{s}_1 - \vec{s}_0)^T R_n^{-1} \vec{y} \) to a threshold:
where \( \eta_0 \) is a scalar value that determines the boundary between the regions where \( H_0 \) and \( H_1 \) are favored.
Decision Boundary and Decision Region#
To better understand the decision rule, let’s consider the geometric interpretation:
Measurement Vector \( \vec{y} \): Represents a point in \( \mathbb{R}^k \).
Weighted Sum \( T(\vec{y}) \):
This is a hyperplane, which is the set of points where \( T(\vec{y}) = \eta_0 \) forms a hyperplane in \( \mathbb{R}^k \).
Decision Boundary: This hyperplane separates the space into two regions:
Above the Hyperplane: \( T(\vec{y}) > \eta_0 \), favoring \( H_1 \).
Below the Hyperplane: \( T(\vec{y}) \leq \eta_0 \), favoring \( H_0 \).
Orientation of Hyperplane:
Normal Vector: \( (\vec{s}_1 - \vec{s}_0)^T R_n^{-1} \), determining the direction orthogonal to the hyperplane.
Position: Shifted by \( \eta_0 \), which depends on the signal differences and noise covariance.
Neyman-Pearson (NP) Criterion#
The Neyman-Pearson (NP) criterion is the appropriate choice when:
Prior Probabilities: There is no information about the prior probabilities of the hypotheses (i.e., we don’t know how likely \( H_0 \) or \( H_1 \) is a priori).
Costs: There is no information about the cost of different types of errors (i.e., no specified cost for false alarms or missed detections).
In such cases, the NP criterion provides an optimal framework for setting the decision rule.
Determine \( \eta_{NP} \) by solving:
Numerical Results#
Simulation steps:
Define Parameters: Set up signal vectors, noise covariance, and other parameters.
Generate Data: Create synthetic measurements under both hypotheses.
Compute Statistics: Calculate \( L(\vec{y}) \) or \( \ell(\vec{y}) \) for all samples.
Determine Threshold: Use a desired \( P_{FA} \) to set the threshold.
Make Decisions: Classify each sample based on the decision rule.
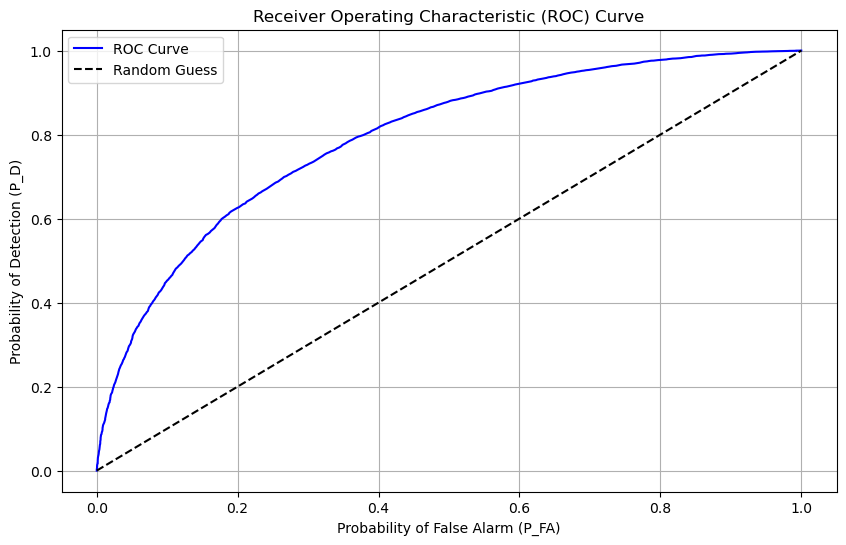
Evaluate Performance: Compute \( P_D \) and \( P_{FA} \), and plot the ROC curve.
import numpy as np
from scipy.linalg import toeplitz, inv
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
# 1. Define Problem Parameters
k = 2 # Dimension for 2D visualization
s0 = np.array([0, 0]) # Hypothesis H0: No signal
s1 = np.array([1, 1]) # Hypothesis H1: Signal present
rho = 0.5 # Correlation coefficient between measurements
Rn = toeplitz([1, rho]) # Noise covariance matrix
Rn_inv = inv(Rn) # Inverse of Rn
N = 10000 # Number of samples per hypothesis
# 2. Generate Synthetic Data
np.random.seed(42) # For reproducibility
noise_H0 = np.random.multivariate_normal(mean=np.zeros(k), cov=Rn, size=N)
noise_H1 = np.random.multivariate_normal(mean=np.zeros(k), cov=Rn, size=N)
y_H0 = s0 + noise_H0 # Under H0
y_H1 = s1 + noise_H1 # Under H1
# 3. Compute the Test Statistic (Log-Likelihood Ratio)
const_term = 0.5 * (s0.T @ Rn_inv @ s0 - s1.T @ Rn_inv @ s1)
w = s1 - s0 # Weight vector
test_stat_H0 = (w @ Rn_inv @ y_H0.T)
test_stat_H1 = (w @ Rn_inv @ y_H1.T)
ell_H0 = test_stat_H0 + const_term
ell_H1 = test_stat_H1 + const_term
# 4. Implement the Decision Rule and Compute ROC
thresholds = np.linspace(min(ell_H0.min(), ell_H1.min()),
max(ell_H0.max(), ell_H1.max()), 1000)
P_FA = [] # Probability of False Alarm
P_D = [] # Probability of Detection
for eta_L in thresholds:
# Decisions for H0 samples
decisions_H0 = ell_H0 > eta_L
P_FA.append(np.mean(decisions_H0)) # False Alarm rate
# Decisions for H1 samples
decisions_H1 = ell_H1 > eta_L
P_D.append(np.mean(decisions_H1)) # Detection rate
# Convert lists to numpy arrays for plotting
P_FA = np.array(P_FA)
P_D = np.array(P_D)
# 5. Plot ROC Curve
plt.figure(figsize=(10, 6))
plt.plot(P_FA, P_D, label='ROC Curve', color='blue')
plt.plot([0, 1], [0, 1], 'k--', label='Random Guess')
plt.xlabel('Probability of False Alarm (P_FA)')
plt.ylabel('Probability of Detection (P_D)')
plt.title('Receiver Operating Characteristic (ROC) Curve')
plt.legend()
plt.grid(True)
plt.show()
# 6. Find and Visualize the Optimal Threshold
desired_P_FA = 0.05 # 5% False Alarm
idx = np.argmin(np.abs(P_FA - desired_P_FA))
optimal_eta_L = thresholds[idx]
optimal_P_D = P_D[idx]
actual_P_FA = P_FA[idx]
print(f"Desired P_FA: {desired_P_FA}")
print(f"Selected Threshold (eta_L): {optimal_eta_L:.4f}")
print(f"Actual P_FA: {actual_P_FA:.4f}")
print(f"Corresponding P_D: {optimal_P_D:.4f}")
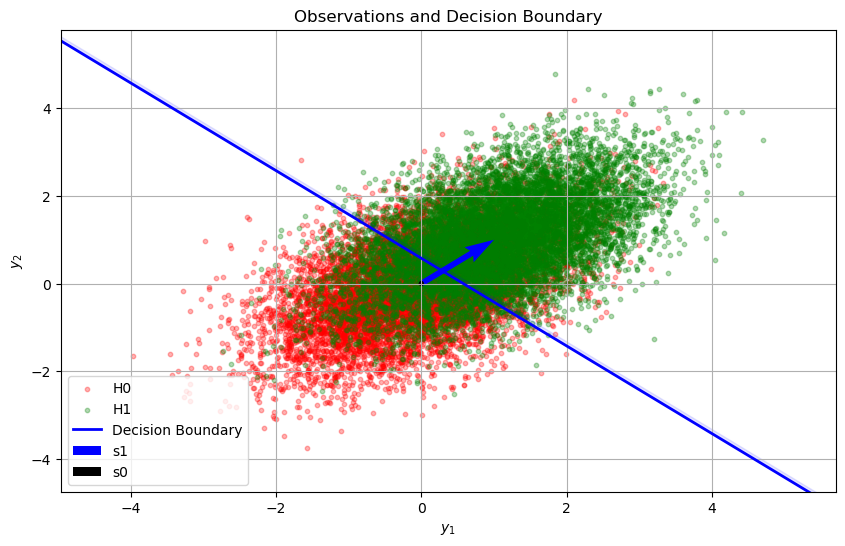
# 7. Plot Observations and Decision Boundary
eta0 = optimal_eta_L + const_term # Adjust threshold based on constants
# Define the decision boundary: w^T y = eta0
# In 2D, solve for y2: y2 = (eta0 - w1 * y1) / w2
y1_min = min(y_H0[:,0].min(), y_H1[:,0].min()) - 1
y1_max = max(y_H0[:,0].max(), y_H1[:,0].max()) + 1
y1_vals = np.linspace(y1_min, y1_max, 100)
if w[1] != 0:
y2_vals = (eta0 - w[0] * y1_vals) / w[1]
else:
y2_vals = np.full_like(y1_vals, eta0 / w[1])
# Plot observations and decision boundary
plt.figure(figsize=(10, 6))
# Plot H0 observations
plt.scatter(y_H0[:,0], y_H0[:,1], alpha=0.3, label='H0', color='red', s=10)
# Plot H1 observations
plt.scatter(y_H1[:,0], y_H1[:,1], alpha=0.3, label='H1', color='green', s=10)
# Plot decision boundary
plt.plot(y1_vals, y2_vals, 'b-', linewidth=2, label='Decision Boundary')
# Optional: Shade regions (above boundary favors H1, below favors H0)
plt.fill_between(y1_vals, y2_vals, y2_vals + 0.1, color='blue', alpha=0.1)
# Plot signal vectors for reference
plt.quiver(0, 0, s1[0], s1[1], angles='xy', scale_units='xy', scale=1, color='blue', label='s1')
plt.quiver(0, 0, s0[0], s0[1], angles='xy', scale_units='xy', scale=1, color='black', label='s0')
plt.xlabel('$y_1$')
plt.ylabel('$y_2$')
plt.title('Observations and Decision Boundary')
plt.legend()
plt.grid(True)
plt.xlim(y1_min, y1_max)
plt.ylim(y_H0[:,1].min()-1, y_H1[:,1].max()+1)
plt.show()
Desired P_FA: 0.05
Selected Threshold (eta_L): 1.2437
Actual P_FA: 0.0501
Corresponding P_D: 0.3129