Channel Capacity#
Channel capacity represents the fundamental limit of a communication channel, defining the maximum rate at which information can be transmitted with an arbitrarily small probability of error.
Channel Capacity of DMC#
For a discrete memoryless channel (DMC), such as the binary symmetric channel (BSC) with crossover probability \(p\) (the probability of a bit being flipped), the capacity is closely tied to the channel’s error characteristics.
Specifically, for the BSC, the capacity is
where
is the binary entropy function. \(H_b(p)\) measures the uncertainty in a binary random variable with probability \(p\).
Consequently, \(1 - H_b(p)\) quantifies the maximum rate (in bits per channel use) at which reliable communication is possible over the BSC, capturing the reduction in uncertainty about the input given the output.
General Definition of Channel Capacity#
More generally, the capacity \(C\) of any channel is defined as
where \(I(X; Y)\) is the mutual information between the input random variable \(X\) (with alphabet \(\mathcal{X}\)) and the output random variable \(Y\) (with alphabet \(\mathcal{Y}\)).
Formally,
where \(p(x,y) = p(x)\,P[y \mid x]\), \(p(x)\) is the input probability mass function (PMF), and \(P[y \mid x]\) is the conditional probability of \(y\) given \(x\).
The maximization is performed over all possible input PMFs \(\vec{p} = (p_1, p_2, \ldots, p_{|\mathcal{X}|})\), subject to:
ensuring \(\vec{p}\) is a valid PMF.
The resulting capacity \(C\), in bits per channel use (assuming base-2 logarithms), is the highest achievable rate at which the error probability can be made arbitrarily small through appropriate coding.
Units of Channel Capacity#
Bits per transmission (bits/channel use) if \(\log_2\) is used. This is standard in digital communication.
Nats per transmission if the natural logarithm (\(\ln\), base \(e\)) is used, where \(1 \text{ nat} \approx 1.443 \text{ bits}\).
If the channel transmits one symbol every \(t_s\) seconds, then the capacity in bits per second or nats per second is \(\tfrac{C}{t_s}\). This expresses the rate on a time-based rather than a per-use basis, which is important for continuous transmission.
Shannon’s Noisy Channel Coding Theorem#
Shannon’s Second Theorem (1948), also known as the Noisy Channel Coding Theorem, underpins the concept of channel capacity:
Noisy Channel Coding Theorem#
Reliable communication over a DMC is possible if the transmission rate \(R\) (in bits per channel use) is less than \(C\). Conversely, if \(R > C\), reliable communication is impossible, because the error probability cannot be made arbitrarily small regardless of the coding scheme.
It means that there exists a coding scheme (often with sufficiently long block codes) that achieves negligible error for \(R < C\), but no such scheme exists for \(R > C\).
This result establishes \(C\) as the ultimate limit for reliable communication and provides a theoretical benchmark against which practical systems are measured.
It also guides the design of error-correcting codes and modulation schemes, ensuring transmission rates do not exceed the channel’s fundamental capabilities.
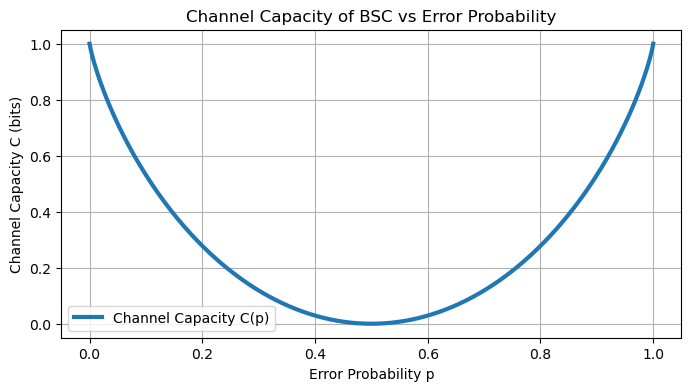
Example: Capacity of the Binary Symmetric Channel (BSC)#
This example is based on [Proakis’s book, Example 6.5-1].
For the BSC with \(\mathcal{X} = \mathcal{Y} = \{0, 1\}\) and crossover probability \(p\) (the probability of a bit being flipped), the capacity is maximized by using a uniform input distribution, i.e., \(P[X = 0] = P[X = 1] = \tfrac{1}{2}\).
Due to the channel’s symmetry:
Output entropy:
\[ H(Y) = H_b\bigl(P[Y = 1]\bigr) = H_b\!\Bigl(\tfrac{1}{2}p + \tfrac{1}{2}(1 - p)\Bigr) = H_b\!\bigl(\tfrac{1}{2}\bigr) = 1. \](Since \(P[Y = 1] = \tfrac{1}{2}p + \tfrac{1}{2}(1 - p) = \tfrac{1}{2}\).)
Conditional entropy:
\[ H(Y \mid X) = P[X = 0] \, H(Y \mid X = 0) + P[X = 1] \, H(Y \mid X = 1) = \tfrac{1}{2}H_b(p) + \tfrac{1}{2}H_b(p) = H_b(p), \]since \(H(Y \mid X = 0) = H(Y \mid X = 1) = H_b(p)\) by symmetry.
Hence,
Expanding \(H_b(p)\) as \(-p \log_2 p - (1 - p)\log_2 (1 - p)\), we get
Special Cases
\(p = 0\) (no errors): \(H_b(0) = 0 \implies C = 1\) bit/channel use (the maximum for a binary channel).
\(p = \tfrac{1}{2}\) (completely random output): \(H_b(\tfrac{1}{2}) = 1 \implies C = 0\), meaning no information is transmitted (the input and output are independent).
For \(p > \tfrac{1}{2}\), one can simply relabel the outputs (interpreting \(0\) as \(1\) and vice versa), reducing the effective \(p\) to \(1 - p\). This shows \(C\) is symmetric about \(p = \tfrac{1}{2}\).
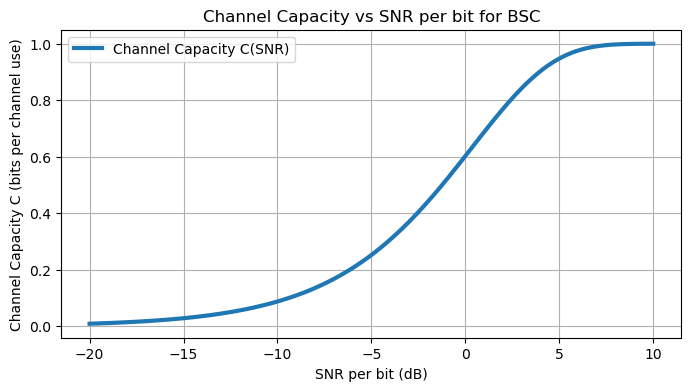
When plotted against the signal-to-noise ratio (SNR) per bit, typically denoted \(E_b/N_0\), the capacity \(C\) increases monotonically, indicating better reliability as SNR rises.
In practical analyses (e.g., BPSK modulation), the crossover probability \(p\) is related to SNR via the error function.
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import erfc
# Small epsilon to avoid log(0) issues
epsilon = 1e-12
# --- Part 1: Capacity vs Error Probability p ---
# Range of error probabilities from 0 to 1
p = np.linspace(0, 1, 1000)
# Adjust p to avoid log(0) by replacing 0 and 1 with near values
p_adjusted = np.where(p == 0, epsilon, np.where(p == 1, 1 - epsilon, p))
# Binary entropy function H_b(p)
H_b = -p_adjusted * np.log2(p_adjusted) - (1 - p_adjusted) * np.log2(1 - p_adjusted)
# Channel capacity C = 1 - H_b(p)
C = 1 - H_b
# Plot C vs p
plt.figure(figsize=(8, 4))
plt.plot(p, C, label='Channel Capacity C(p)', linewidth=3)
plt.xlabel('Error Probability p')
plt.ylabel('Channel Capacity C (bits)')
plt.title('Channel Capacity of BSC vs Error Probability')
plt.grid(True)
plt.legend()
plt.show()
# --- Part 2: Capacity vs SNR ---
# Define SNR range in dB
SNR_dB = np.arange(-20, 10.1, 0.1) # From -20 dB to 10 dB
SNR = 10 ** (SNR_dB / 10) # Convert dB to linear scale
# Preallocate capacity array
C_snr = np.zeros_like(SNR)
# Calculate capacity for each SNR value
for i, snr in enumerate(SNR):
# Error probability p using Q-function: Q(x) = 0.5 * erfc(x / sqrt(2))
p = 0.5 * erfc(np.sqrt(2 * snr) / np.sqrt(2)) # Q(sqrt(2 * SNR))
# Adjust p to avoid log(0)
p = max(epsilon, min(1 - epsilon, p))
# Binary entropy H_b(p)
H_p = -p * np.log2(p) - (1 - p) * np.log2(1 - p)
# Capacity
C_snr[i] = 1 - H_p
# Plot C vs SNR
plt.figure(figsize=(8, 4))
plt.plot(SNR_dB, C_snr, label='Channel Capacity C(SNR)', linewidth=3)
plt.xlabel('SNR per bit (dB)')
plt.ylabel('Channel Capacity C (bits per channel use)')
plt.title('Channel Capacity vs SNR per bit for BSC')
plt.grid(True)
plt.legend()
plt.show()
Capacity of the Discrete-Time Binary-Input AWGN Channel#
We consider a binary-input additive white Gaussian noise (AWGN) channel with inputs \(X = \pm A\) (e.g., BPSK signaling) and continuous output \(Y = X + N\), where \(N \sim \mathcal{N}(0,\sigma^2)\).
The conditional probability density function (PDF) is
By symmetry, the capacity is again maximized by a uniform input PMF: \(P[X = A] = P[X = -A] = \tfrac{1}{2}\).
Then, the channel capacity is
However, computing \(C\) directly from the continuous output \(Y\) is more conveniently done using:
with \(P(x) = \tfrac{1}{2}\). Thus,
where
is the overall output PDF.
Simplified Form and Behavior#
While the integral does not have a simple closed-form solution, it can be written as
where
and \(x = \tfrac{A}{\sigma}\) is the signal-to-noise amplitude ratio.
Due to symmetry (\(g(-x)\) relates closely to \(g(x)\)), the capacity depends on \(\tfrac{A^2}{\sigma^2}\), often expressed as \(\tfrac{E_b}{N_0}\) (energy per bit to noise power spectral density ratio) in communication systems.
As \(\tfrac{E_b}{N_0}\) increases, \(C\) grows from 0 (at very low SNR) to 1 bit per symbol (at high SNR), reflecting the channel’s ability to approach error-free operation.
For example, for target rates \(R = \tfrac{1}{2}\) or \(\tfrac{1}{3}\), specific \(\tfrac{E_b}{N_0}\) thresholds (e.g., 0.188 dB and \(-0.496\) dB) indicate the minimum required SNR—these values are typically found via numerical methods or simulation.
This discussion provides a comprehensive view of how channel capacity is defined and computed for the BSC and for a binary-input AWGN channel, highlighting its central role in designing reliable communication systems.
Capacity of Symmetric Channels#
In certain channel models—such as the Binary Symmetric Channel (BSC) and the binary-input AWGN channel—the channel transition probabilities exhibit symmetry.
A symmetric channel is characterized by a transition probability matrix \(\vec{p} = [P(y_j \mid x_i)]\) that satisfies:
Each row of \(\vec{p}\) is a permutation of any other row.
Each column of \(\vec{p}\) is a permutation of any other column.
As an example, the BSC with crossover probability \(p\) has transition matrix
Row 1, \((1 - p, \, p)\), is a permutation of Row 2, \((p, \, 1 - p)\), and similarly for the columns.
This symmetry implies that the channel treats all inputs equivalently up to a possible relabeling of outputs.
Capacity of Symmetric Channels Under a Uniform Input#
For symmetric channels, the capacity-achieving input distribution is uniform, i.e., \(P[x_i] = 1 / |\mathcal{X}|\) for each \(x_i \in \mathcal{X}\).
The resulting capacity is
where \(\bigl|\mathcal{Y}\bigr|\) is the size of the output alphabet, and \(\vec{p} = (p_1, p_2, \ldots, p_{|\mathcal{Y}|})\) is any row of the transition matrix \(\vec{p}\).
Because each row is just a permutation of the others, \(\vec{p}\) has the same entropy regardless of which row is chosen:
Thus, for the BSC (\(\mathcal{X} = \mathcal{Y} = \{0,1\}\)) with crossover probability \(p\), each row is \((p,\,1 - p)\) or \((1 - p,\,p)\). Since \(\bigl|\mathcal{Y}\bigr| = 2\), we get
confirming the known BSC capacity.
It is noted that output symmetry (as in binary-input AWGN) is sufficient to guarantee a uniform capacity-achieving input, even if the channel does not have a finite transition matrix.
Conditions for Capacity-Achieving Distributions#
For a general discrete memoryless channel (DMC), the capacity
is achieved by an input distribution \(\{P[x]\}\) that satisfies the following (sometimes referred to as the Kuhn–Tucker conditions in information theory):
\(I(x; Y) = C\) for all \(x \in \mathcal{X}\) with \(P[x] > 0\).
\(I(x; Y) \le C\) for all \(x \in \mathcal{X}\) with \(P[x] = 0\).
Here, the pointwise mutual information is
and
These conditions ensure that:
For any input \(x\) that is actually used (i.e., \(P[x] > 0\)), the information rate \(I(x; Y)\) must equal the channel capacity \(C\).
If an input \(x\) is not used (i.e., \(P[x] = 0\)), its information rate cannot exceed \(C\).
In symmetric channels, the uniform distribution satisfies these conditions because \(I(x; Y)\) is the same for all \(x\).
For non-symmetric channels, finding the optimal distribution often requires iterative methods (e.g., the Blahut–Arimoto algorithm) if uniform inputs do not satisfy the conditions.
Capacity of the Discrete-Time AWGN Channel (Power-Constrained)#
Consider a discrete-time AWGN channel:
where \(N_i\) are i.i.d. Gaussian random variables with mean 0 and variance \(\sigma^2\).
The inputs \(\{X_i\}\) must satisfy the average power constraint
Sphere Packing Argument#
For \(n\) uses of the channel, the transmitted vector \(\vec{x} = (x_1, \ldots, x_n)\) must lie within an \(n\)-dimensional sphere of radius \(\sqrt{nP}\).
Because the noise vector \(\vec{n} = (n_1,\ldots,n_n)\) is Gaussian, the received vector
lies in a sphere of radius \(\sqrt{n(P + \sigma^2)}\).
Approximating the maximum number of distinguishable codewords (messages) by the ratio of volumes leads to
Hence, the achievable rate (in bits per channel use) is
This is precisely the channel capacity for an average power constraint \(P\).
Achievability follows by choosing \(X\) to be Gaussian \(\mathcal{N}(0, P)\), which maximizes \(I(X;Y)\).
Formally,
where \(h(\cdot)\) denotes differential entropy, and \(X\sim\mathcal{N}(0,P)\) maximizes \(h(Y)\).
It is noted that the capacity is in bits per channel use, and can be converted to bits per second by multiplying with the sampling rate.
Capacity of the Band-Limited Waveform AWGN Channel (Power-Constrained)#
Now consider a continuous-time AWGN channel with:
Bandwidth \(W\).
Input power constraint \(\mathbb{E}[x^2(t)] \le P\).
Noise power spectral density \(N_0/2\).
It can be shown (via sampling or dimensionality arguments) that this setup is equivalent to \(2W\) discrete-time uses per second of an AWGN channel with:
Power constraint per use: \(\tfrac{P}{2W}\).
Noise variance: \(\sigma^2 = \tfrac{N_0}{2}\).
Per-Use Capacity#
The discrete-time channel capacity per use is
Because there are \(2W\) uses per second, the total channel capacity in bits per second is
This is Shannon’s well-known capacity formula for a band-limited AWGN channel.
The term \(\tfrac{P}{N_0\,W}\) is the signal-to-noise ratio (SNR).
Capacity Behavior#
Increasing Power \(P\):
As \(P \to \infty\), capacity \(C \to \infty\).However, the increase is logarithmic (\(\log_2(1 + x)\approx\log_2 x\) for large \(x\)), meaning there are diminishing returns from simply increasing power.
Increasing Bandwidth \(W\):
Positive effect: More uses per second (\(2W\)) increase capacity.
Negative effect: Increasing \(W\) lowers SNR \(\bigl(\tfrac{P}{N_0W}\bigr)\), because the noise power is proportional to \(W\).
For fixed \(P\), letting \(W\to\infty\):
\[ \lim_{W\to\infty} W\,\log_2\!\Bigl(1 + \tfrac{P}{N_0\,W}\Bigr). \]Using \(\ln(1 + x)\approx x\) for small \(x\), we get
\[ \log_2\!\Bigl(1 + \tfrac{P}{N_0\,W}\Bigr) = \frac{\ln\!\bigl(1 + \tfrac{P}{N_0\,W}\bigr)}{\ln 2} \approx \frac{\tfrac{P}{N_0\,W}}{\ln 2}. \]Hence,
\[ C_{\infty} \approx W \times \frac{\tfrac{P}{N_0\,W}}{\ln 2} = \frac{P}{N_0}\,\frac{1}{\ln 2} = \frac{P}{N_0}\,\log_2 e \approx 1.44\,\frac{P}{N_0}. \]So, infinite bandwidth yields a finite limiting capacity, determined by \(\frac{P}{N_0}\).
Bandwidth Efficiency of Band-Limited Waveform AWGN Channel with Power Constraint#
The bandwidth efficiency of a communication system quantifies how effectively the available bandwidth is utilized to transmit data.
It is defined as the ratio of the bit rate \(R\) (in bits per second, b/s) to the bandwidth \(W\) (in Hertz, Hz):
Often denoted by \(r\), this metric indicates the number of bits transmitted per unit of bandwidth and thus provides insight into the spectral efficiency of a signaling scheme.
To investigate the trade-off between bandwidth efficiency and power efficiency, we begin with the capacity of a band-limited AWGN channel under power constraint \(P\) and noise power spectral density \(N_0/2\):
For reliable communication, the bit rate \(R\) must satisfy \(R < C\), ensuring that errors can be made arbitrarily small through suitable coding techniques.
Substituting the expression for \(C\) into \(R < C\):
Dividing both sides by the bandwidth \(W\) yields
Since \(r = \tfrac{R}{W}\), we obtain
This inequality reveals a fundamental relationship between the bandwidth efficiency \(r\) and the SNR \(\tfrac{P}{N_0\,W}\), identifying the maximum achievable \(r\) for given values of power \(P\) and bandwidth \(W\).
Relating Bandwidth Efficiency to Power Efficiency#
To express this connection in terms of power efficiency, we introduce the energy per bit to noise power spectral density ratio, \(\tfrac{E_b}{N_0}\).
For a signaling scheme with bit rate \(R\) and power \(P\), the total energy per symbol \(E\) is linked to the symbol duration \(T_s = \tfrac{1}{R}\) (assuming one symbol per bit for simplicity):
For \(M\)-ary signaling, \(R = \tfrac{\log_2 M}{T_s}\), but here we focus directly on the bit rate.
In that case,
Hence,
Substitute \(P\) into the earlier capacity inequality \(r < \log_2\!\bigl(1 + \tfrac{P}{N_0\,W}\bigr)\):
since \(\tfrac{R}{W} = r\). Rearranging this:
This formula specifies the minimum \(\tfrac{E_b}{N_0}\) required for reliable communication at a given bandwidth efficiency \(r\).
It demonstrates that higher \(r\) (i.e., more bits per Hz) necessitates greater power efficiency, underscoring the trade-off between spectral resources and power resources.
Minimum \(\tfrac{E_b}{N_0}\) for Reliable Communication#
To identify the absolute minimum \(\tfrac{E_b}{N_0}\) that enables reliable transmission, we examine the limiting case \(r \to 0\) (vanishingly small bandwidth efficiency). From
use the Taylor expansion \(2^r = e^{r\,\ln 2} \approx 1 + r\,\ln 2\) for small \(r\). Thus,
Therefore,
This is known as the Shannon limit, representing the fundamental boundary below which no communication system can achieve arbitrarily low error probability.
Converting to decibels via \(10 \log_{10}(0.693) \approx -1.6\,\text{dB}\), we see this limit applies to any physical communication scheme.
Reaching the limit requires \(r \to 0\), which corresponds to \(W \to \infty\) when \(R\) is fixed; effectively, one leverages vast bandwidth to reduce the SNR per Hz but compensates with sophisticated coding across many dimensions.
Achieving Capacity With Orthogonal Signals#
Next, consider a system employing \(M\) orthogonal waveforms (e.g., frequency-shift keying, FSK) over an AWGN channel. The probability of error \(P_e\) when distinguishing among \(M\) signals, each having energy \(E = P\,T_s\), is
where
is the Gaussian tail function, and \(\sqrt{\tfrac{2E}{N_0}}\) is the signal amplitude that depends on the SNR.
Since this integral typically lacks a closed-form solution, it is evaluated numerically to assess error performance as a function of \(\tfrac{E}{N_0}\).
Infinite Bandwidth Scenario#
When \(W \to \infty\), the channel capacity approaches
as derived from the infinite-bandwidth limit.
If we let \(M \to \infty\) (with \(T\) denoting the signaling duration), the bit rate \(R\) can approach various fractions of \(C_\infty\).
Upper bounds on \(P_e\) are often given for two regimes:
Low-rate regime \(\bigl(0 \le R \le \tfrac{1}{4}C_\infty\bigr)\):
The exponent \(\tfrac{1}{2}C_\infty - R\) remains positive if \(R < \tfrac{1}{2}C_\infty\). As \(T \to \infty\) (and thus \(M = \tfrac{R\,T}{\log_2 M}\) becomes large), \(P_e \to 0\).High-rate regime \(\bigl(\tfrac{1}{4}C_\infty \le R \le C_\infty\bigr)\):
The exponent \(\bigl(\sqrt{C_\infty} - \sqrt{R}\bigr)^2\) is positive if \(R < C_\infty\). Again, \(P_e \to 0\) with \(T \to \infty\).
Since \(C_\infty = \tfrac{P}{N_0 \ln 2}\), reliable communication is possible whenever \(R < C_\infty\), and the error probability \(P_e\) decreases exponentially as \(T\) increases.
Orthogonal signaling can achieve this capacity in the limit \(M \to \infty\) by exploiting the large-dimensional signal space, thereby approaching the Shannon limit \(\tfrac{E_b}{N_0} = \ln 2\).