Example: Antipodal Signal Detection using Multiple Samples

Example: Antipodal Signal Detection using Multiple Samples#

As consider in Chapter 2, we are dealing with a signal detection problem where we need to decide between two hypotheses based on observed data corrupted by noise.

Specifically, we’re considering antipodal signals, meaning the signals under the two hypotheses are negatives of each other. Here’s a summary of the given information:

Signals:

Under hypothesis $ H_0 $: $ s_0 = -b $
Under hypothesis $ H_1 $: $ s_1 = b $
$ b > 0 $ ensures that $ s_0 $ and $ s_1 $ are indeed antipodal.

Prior Probabilities:

$ \pi_0 = 0.8 $ (probability of $ H_0 $)
$ \pi_1 = 0.2 $ (probability of $ H_1 $)

Noise Model:

The noise $ \mathbf{n} $ is Gaussian with zero mean and variance $ \sigma^2 $.
Probability Density Function (pdf) of noise:

\[ p_{\mathbf{n}}(n) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{n^2}{2\sigma^2} \right) \]

Extension to Multiple Samples:

Instead of a single observation, we have $ k $ independent samples.

Step 1: Conditional PDFs Extending to $ k $ Independent Samples#

Since $ n_i $ is Gaussian with zero mean and variance $ \sigma^2 $, each $ y_i $ conditioned on the hypothesis is also Gaussian:

Conditional PDFs:

\[ p(y_i | H_0) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{(y_i - (-b))^2}{2\sigma^2} \right) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{(y_i + b)^2}{2\sigma^2} \right) \]

\[ p(y_i | H_1) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{(y_i - b)^2}{2\sigma^2} \right) \]

Extending to $ k $ Independent Samples

Assuming that each of the $ k $ samples is independent, the joint probability density function (pdf) for all samples under each hypothesis is the product of individual PDFs.

Under $ H_0 $:

\[ p(\vec{y} | H_0) = \prod_{i=1}^k p(y_i | H_0) = \prod_{i=1}^k \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{(y_i + b)^2}{2\sigma^2} \right) \]

Simplifying the product:

\[\begin{split} \begin{align} p(\vec{y} | H_0) &= \left( \frac{1}{\sqrt{2\pi\sigma^2}} \right)^k \exp\left( -\frac{\sum_{i=1}^k (y_i + b)^2}{2\sigma^2} \right) \\ &= \frac{1}{(2\pi\sigma^2)^{k/2}} \exp\left( -\frac{\sum_{i=1}^k (y_i + b)^2}{2\sigma^2} \right) \end{align} \end{split}\]

Under $ H_1 $:

\[ p(\vec{y} | H_1) = \prod_{i=1}^k p(y_i | H_1) = \prod_{i=1}^k \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{(y_i - b)^2}{2\sigma^2} \right) \]

Simplifying similarly:

\[ p(\vec{y} | H_1) = \frac{1}{(2\pi\sigma^2)^{k/2}} \exp\left( -\frac{\sum_{i=1}^k (y_i - b)^2}{2\sigma^2} \right) \]

Step 2: Computing the Likelihood Ratio#

The likelihood ratio $ L(\vec{y}) $ is the ratio of the likelihoods under $ H_1 $ and $ H_0 $:

\[ \boxed{ L(\vec{y}) = \frac{p(\vec{y} | H_1)}{p(\vec{y} | H_0)} } \]

Substituting the expressions derived:

\[ L(\vec{y}) = \frac{\frac{1}{(2\pi\sigma^2)^{k/2}} \exp\left( -\frac{\sum_{i=1}^k (y_i - b)^2}{2\sigma^2} \right)}{\frac{1}{(2\pi\sigma^2)^{k/2}} \exp\left( -\frac{\sum_{i=1}^k (y_i + b)^2}{2\sigma^2} \right)} \]

Simplifying:

\[ L(\vec{y}) = \exp\left( \frac{\sum_{i=1}^k (y_i + b)^2 - \sum_{i=1}^k (y_i - b)^2}{2\sigma^2} \right) \]

Simplifying the Exponent

Let’s simplify the exponent:

\[ \sum_{i=1}^k (y_i + b)^2 - \sum_{i=1}^k (y_i - b)^2 \]

Expanding each squared term:

\[ (y_i + b)^2 = y_i^2 + 2by_i + b^2 \]

\[ (y_i - b)^2 = y_i^2 - 2by_i + b^2 \]

Subtracting the two:

\[ (y_i + b)^2 - (y_i - b)^2 = (y_i^2 + 2by_i + b^2) - (y_i^2 - 2by_i + b^2) = 4by_i \]

Therefore, for all $ k $ samples:

\[ \sum_{i=1}^k (y_i + b)^2 - \sum_{i=1}^k (y_i - b)^2 = \sum_{i=1}^k 4by_i = 4b \sum_{i=1}^k y_i \]

Substituting back into the expression for $ L(\vec{y}) $:

\[ \boxed{ L(\vec{y}) = \exp\left( \frac{4b \sum_{i=1}^k y_i}{2\sigma^2} \right) = \exp\left( \frac{2b}{\sigma^2} \sum_{i=1}^k y_i \right) } \]

Log-Likelihood Ratio#

Taking the natural logarithm of the likelihood ratio simplifies analysis, especially for threshold-based decision rules.

\[ \boxed{ \ell(\vec{y}) = \ln L(\vec{y}) = \frac{2b}{\sigma^2} \sum_{i=1}^k y_i } \]

Step 3: Make Decision#

To make a decision between $ H_0 $ and $ H_1 $, we compare the likelihood ratio (or log-likelihood ratio) to a threshold.

Threshold Setting:

Determine a threshold $ \eta $ using Bayes, MAP, MiniMax, Neyman-Pearson

One common approach is the Neyman-Pearson criterion, which maximizes the probability of detection for a given probability of false alarm $ P_f $.

For example: $ P_f = P(L(\vec{y}) > \eta | H_0) = 0.1 $.

Alternatively, using the log-likelihood ratio:

\[ \ell(\vec{y}) > \ln \eta \]

Decision Rule:

If $ L(\vec{y}) > \eta $ (or $ \ell(\vec{y}) > \ln \eta $), decide $ H_1 $.
Otherwise, decide $ H_0 $.

Neyman-Pearson (NP) Criterion#

Since there is no information about the cost of different types of errors (i.e., no specified cost for false alarms or missed detections), the Neyman-Pearson (NP) criterion is the appropriate choice.

The theoretical derivation of the Neyman-Pearson threshold ($ \eta_{\text{NP}} $) and the probability of detection ($ P_d $) using the specified parameters:

Signal Amplitude ($ b $): 0.5
Noise Standard Deviation ($ \sigma $): 2.0
Number of Samples ($ k $): 2
Desired Probability of False Alarm ($ P_f $): 0.1

Derivation of the Neyman-Pearson Threshold ($ \eta_{\text{NP}} $)#

Expressing the Log-Likelihood Ratio

Under both hypotheses, the log-likelihood ratio can be derived as follows:

\[ \ell(\vec{y}) = \ln\left( \frac{p(\vec{y} | H_1)}{p(\vec{y} | H_0)} \right) = \frac{2b}{\sigma^2} \sum_{i=1}^k y_i \]

Thus, the decision rule becomes:

\[ \frac{2b}{\sigma^2} \sum_{i=1}^k y_i \underset{H_0}{\overset{H_1}{\gtrless}} \ln(\eta_{\text{NP}}) \]

Solving for the sum of observations:

\[ \sum_{i=1}^k y_i \underset{H_0}{\overset{H_1}{\gtrless}} \frac{\sigma^2}{2b} \ln(\eta_{\text{NP}}) \]

Let’s denote the threshold on the sum as $ S_{\text{threshold}} $:

\[ \boxed{ S_{\text{threshold}} = \frac{\sigma^2}{2b} \ln(\eta_{\text{NP}}) } \]

Determining $ \eta_{\text{NP}} $ for $ P_f = 0.1 $

To achieve a desired Probability of False Alarm ($ P_f $) of 0.1, we set:

\[ P\left( \sum_{i=1}^k y_i > S_{\text{threshold}} \bigg| H_0 \right) = 0.1 \]

Under $ H_0 $, each $ y_i $ is normally distributed as $ \mathcal{N}(-b, \sigma^2) $.

Therefore, the sum $ S = \sum_{i=1}^k y_i $ is also normally distributed:

\[ S \sim \mathcal{N}(-k b, k \sigma^2) \]

Finding $ S_{\text{threshold}} $

To find the threshold corresponding to $ P_f = 0.1 $:

Standardize $ S $:

\[ Z = \frac{S - (-k b)}{\sigma \sqrt{k}} \sim \mathcal{N}(0, 1) \]

Determine the z-score for the upper 10% tail:

\[ z_{0.1} = \Phi^{-1}(1 - P_f) = \Phi^{-1}(0.9) \approx 1.2816 \]

Where $ \Phi^{-1} $ is the inverse CDF of the standard normal distribution.

Compute $ S_{\text{threshold}} $:

\[ S_{\text{threshold}} = \mu_{S|H_0} + z_{0.1} \sigma_{S|H_0} = -k b + z_{0.1} \sigma \sqrt{k} \]

Substituting the given parameters:

\[ S_{\text{threshold}} = -2 \times 0.5 + 1.2816 \times 2 \times \sqrt{2} \approx -1.0 + 3.6255 = 2.6255 \]

Solving for $ \eta_{\text{NP}} $

From the relationship between $ S_{\text{threshold}} $ and $ \eta_{\text{NP}} $:

\[ S_{\text{threshold}} = \frac{\sigma^2}{2b} \ln(\eta_{\text{NP}}) \]

Solving for $ \ln(\eta_{\text{NP}}) $:

\[ \ln(\eta_{\text{NP}}) = \frac{2b}{\sigma^2} \times S_{\text{threshold}} = \frac{2 \times 0.5}{4} \times 2.6255 = \frac{1.0}{4} \times 2.6255 = 0.6564 \]

Therefore:

\[ \boxed{ \eta_{\text{NP}} = \exp(0.6564) \approx 1.928 } \]

Derivation of the Probability of Detection ($ P_d $)#

The Probability of Detection ($ P_d $) is the likelihood that the test correctly decides $ H_1 $ when $ H_1 $ is true.

\[ P_d = P\left( \sum_{i=1}^k y_i > S_{\text{threshold}} \bigg| H_1 \right) \]

Distribution Under $ H_1 $

Under $ H_1 $, each $ y_i $ is distributed as $ \mathcal{N}(b, \sigma^2) $. Therefore, the sum $ S = \sum_{i=1}^k y_i $ is normally distributed as:

\[ S \sim \mathcal{N}(k b, k \sigma^2) \]

Calculating $ P_d $

To compute $ P_d $, we standardize $ S $ under $ H_1 $:

\[ Z = \frac{S - \mu_{S|H_1}}{\sigma_{S|H_1}} = \frac{S - k b}{\sigma \sqrt{k}} \sim \mathcal{N}(0, 1) \]

Thus:

\[ P_d = P\left( S > S_{\text{threshold}} \bigg| H_1 \right) = P\left( Z > \frac{S_{\text{threshold}} - k b}{\sigma \sqrt{k}} \right) = 1 - \Phi\left( \frac{S_{\text{threshold}} - k b}{\sigma \sqrt{k}} \right) \]

Substituting $ S_{\text{threshold}} $

Given:

\[ S_{\text{threshold}} = 2.6255 \]

And:

\[ k = 2, \quad b = 0.5, \quad \sigma = 2.0 \]

Calculate the standardized value:

\[ \frac{S_{\text{threshold}} - k b}{\sigma \sqrt{k}} = \frac{2.6255 - 2 \times 0.5}{2 \times \sqrt{2}} = \frac{2.6255 - 1.0}{2.8284} \approx \frac{1.6255}{2.8284} \approx 0.5745 \]

Thus:

\[ \boxed{ P_d = 1 - \Phi(0.5745) \approx 1 - 0.7163 = 0.2837 } \]

Numerical Results#

import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt

# Seed for reproducibility
np.random.seed(42)

# ===============================
# 1. Define Parameters
# ===============================

# Signal parameters
b = 0.5          # Reduced Signal amplitude
sigma = 2.0      # Increased Noise standard deviation
k = 2            # Number of samples

# Prior probabilities
pi_0 = 0.8       # Probability of H0
pi_1 = 0.2       # Probability of H1

# Desired probability of false alarm
P_f_desired = 0.1

# Number of simulations
N_simulations = 100000

# ===============================
# 2. Theoretical Threshold (eta_NP)
# ===============================

# Critical z-value for P_f = 0.1
z_Pf = norm.ppf(1 - P_f_desired)  # Approximately 1.2816 for P_f=0.1

# Compute the threshold sum S_threshold
mu_H0 = -k * b
sigma_H0 = sigma * np.sqrt(k)
S_threshold = mu_H0 + z_Pf * sigma_H0  # Threshold under H0

# Compute ln(eta_NP ) using the decision rule
# ln(eta_NP ) = (2b / sigma^2) * S_threshold
ln_eta_NP_theoretical = (2 * b / sigma**2) * S_threshold

# Theoretical threshold
eta_NP_theoretical = np.exp(ln_eta_NP_theoretical)

print(f"Theoretical ln(eta_NP): {ln_eta_NP_theoretical:.4f}")
print(f"Theoretical eta_NP: {eta_NP_theoretical:.4f}")

# ===============================
# 3. Simulate Observations Under H0 and H1
# ===============================

# Generate noise for H0 and H1
noise_H0 = np.random.normal(loc=0, scale=sigma, size=(N_simulations, k))
noise_H1 = np.random.normal(loc=0, scale=sigma, size=(N_simulations, k))

# Generate observations under H0 and H1
Y_H0 = -b + noise_H0
Y_H1 = b + noise_H1

# ===============================
# 4. Compute Log-Likelihood Ratios
# ===============================

# Compute the sum of observations for each simulation
S_H0 = np.sum(Y_H0, axis=1)
S_H1 = np.sum(Y_H1, axis=1)

# Compute log-likelihood ratios
ell_H0 = (2 * b / sigma**2) * S_H0
ell_H1 = (2 * b / sigma**2) * S_H1

# ===============================
# 5. Determine Empirical Threshold (eta_NP)
# ===============================

# Find the empirical threshold based on H0 simulations
ell_threshold_empirical = np.percentile(ell_H0, 90)  # 90th percentile for P_f=0.1

# Empirical eta_NP
eta_NP_empirical = np.exp(ell_threshold_empirical)

print(f"Empirical log-likelihood ratio threshold: {ell_threshold_empirical:.4f}")
print(f"Empirical eta_NP: {eta_NP_empirical:.4f}")

# ===============================
# 6. Compute Empirical Probability of Detection (P_d)
# ===============================

# Compute P_d
P_d_empirical = np.mean(ell_H1 > ell_threshold_empirical)

print(f"Empirical Probability of Detection P_d: {P_d_empirical:.4f}")

# ===============================
# 7. Compute Theoretical Probability of Detection (P_d)
# ===============================

# Theoretical P_d calculation
# Under H1, S ~ N(k b, k sigma^2 )
mu_H1 = k * b
sigma_H1 = sigma * np.sqrt(k)

# Compute P_d = P(S > S_threshold | H1 )
z = (S_threshold - mu_H1) / sigma_H1
P_d_theoretical = 1 - norm.cdf(z)

print(f"Theoretical Probability of Detection P_d: {P_d_theoretical:.4f}")

Theoretical ln(eta_NP): 0.6562
Theoretical eta_NP: 1.9274
Empirical log-likelihood ratio threshold: 0.6600
Empirical eta_NP: 1.9347
Empirical Probability of Detection P_d: 0.2802
Theoretical Probability of Detection P_d: 0.2828

Real-World Application Example#

Scenario: Signal Detection in Wireless Communication

Context:

Purpose: Determine whether a specific signal is present in the received wireless data.
Application: Deciding whether a user is transmitting data ($ H_1 $) or not ($ H_0 $).

Given Parameters:

Signal Amplitude ($ b $): 0.5 (represents signal strength)
Noise Standard Deviation ($ \sigma $): 2.0 (represents environmental noise)
Number of Samples ($ k $): 2 (e.g., two consecutive data packets)
Desired False Alarm Rate ($ P_f $): 0.1 (10% chance of falsely detecting a signal)

Decision Process:

Receive Data Samples:
- Suppose two data packets are received with signal measurements $ y_1 $ and $ y_2 $.
Compute the Log-Likelihood Ratio:
- Using the formula: $$ \ell(\vec{y}) = 0.25 \times (y_1 + y_2) $$
Apply the Threshold:
- Compare $ \ell(\vec{y}) $ with $ \ln(\eta_{\text{NP}}) \approx 0.6564 $.
Make a Decision:
- If $ \ell(\vec{y}) > 0.6564 $: Decide $ H_1 $ (User is transmitting data).
- Else: Decide $ H_0 $ (No data transmission).

Example 1: Deciding $ H_1 $ (Signal Present)#

Given:

Observed Samples:
- $ y_1 = 2.0 $
- $ y_2 = 3.0 $

Steps:

Compute the Sum of Observations:

\[ S = y_1 + y_2 = 2.0 + 3.0 = 5.0 \]
Calculate the Log-Likelihood Ratio ($ \ell(\vec{y}) $):

\[ \ell(\vec{y}) = 0.25 \times 5.0 = 1.25 \]
Compare with the Threshold $ \ln(\eta_{\text{NP}}) $:
- Given $ \eta_{\text{NP}} \approx 1.928 $, calculate $ \ln(\eta_{\text{NP}}) $:
  
  \[ \ln(1.928) \approx 0.6564 \]
- Check if $ \ell(\vec{y}) > 0.6564 $:
  
  \[ 1.25 > 0.6564 \quad \text{(True)} \]
Decision:
- Since $ \ell(\vec{y}) > \ln(\eta_{\text{NP}}) $, decide $ H_1 $ (signal is present).

Interpretation:

The sum of the observations is sufficiently large to exceed the threshold, indicating the presence of the signal.

Example 2: Deciding $ H_0 $ (No Signal)#

Given:

Observed Samples:
- $ y_1 = -1.0 $
- $ y_2 = 0.0 $

Steps:

Compute the Sum of Observations:

\[ S = y_1 + y_2 = -1.0 + 0.0 = -1.0 \]
Calculate the Log-Likelihood Ratio ($ \ell(\vec{y}) $):

\[ \ell(\vec{y}) = 0.25 \times (-1.0) = -0.25 \]
Compare with the Threshold $ \ln(\eta_{\text{NP}}) $:
- Given $ \ln(\eta_{\text{NP}}) \approx 0.6564 $, check if $ \ell(\vec{y}) > 0.6564 $:
  
  \[ -0.25 > 0.6564 \quad \text{(False)} \]
Decision:
- Since $ \ell(\vec{y}) \leq \ln(\eta_{\text{NP}}) $, decide $ H_0 $ (no signal is present).

Interpretation:

The sum of the observations does not exceed the threshold, suggesting that there is no significant signal present.

Example 3: Edge Case Near the Threshold#

Given:

Observed Samples:
- $ y_1 = 1.0 $
- $ y_2 = 1.0 $

Steps:

Compute the Sum of Observations:

\[ S = y_1 + y_2 = 1.0 + 1.0 = 2.0 \]
Calculate the Log-Likelihood Ratio ($ \ell(\vec{y}) $):

\[ \ell(\vec{y}) = 0.25 \times 2.0 = 0.5 \]
Compare with the Threshold $ \ln(\eta_{\text{NP}}) $:
- Given $ \ln(\eta_{\text{NP}}) \approx 0.6564 $, check if $ \ell(\vec{y}) > 0.6564 $:
  
  \[ 0.5 > 0.6564 \quad \text{(False)} \]
Decision:
- Since $ \ell(\vec{y}) \leq \ln(\eta_{\text{NP}}) $, decide $ H_0 $ (no signal is present).

Interpretation:

The sum of the observations is slightly below the threshold, resulting in a decision in favor of $ H_0 $.

import numpy as np
from scipy.stats import norm

# ===============================
# 1. Define Parameters
# ===============================

# Signal parameters
b = 0.5          # Signal amplitude
sigma = 2.0      # Noise standard deviation
k = 2            # Number of samples

# Desired probability of false alarm
P_f_desired = 0.1

# Neyman-Pearson Threshold (from previous derivation)
eta_NP = 1.928
ln_eta_NP = np.log(eta_NP)  # Approximately 0.6564

# ===============================
# 2. Example Observations
# ===============================

# Define observed samples
# Example 1: Decide H1
y1_H1 = 2.0
y2_H1 = 3.0

# Example 2: Decide H0
y1_H0 = -1.0
y2_H0 = 0.0

# Example 3: Edge Case
y1_edge = 1.0
y2_edge = 1.0

# ===============================
# 3. Compute Log-Likelihood Ratios
# ===============================

def compute_log_likelihood_ratio(y1, y2, b, sigma, k):
    S = y1 + y2
    ell = (2 * b / sigma**2) * S
    return ell

# Compute for Example 1
ell_H1 = compute_log_likelihood_ratio(y1_H1, y2_H1, b, sigma, k)
print(f"Example 1: Observations = ({y1_H1}, {y2_H1})")
print(f"Log-Likelihood Ratio (ell) = {ell_H1:.4f}")
print(f"Decision: {'H1' if ell_H1 > ln_eta_NP else 'H0'}\n")

# Compute for Example 2
ell_H0 = compute_log_likelihood_ratio(y1_H0, y2_H0, b, sigma, k)
print(f"Example 2: Observations = ({y1_H0}, {y2_H0})")
print(f"Log-Likelihood Ratio (ell) = {ell_H0:.4f}")
print(f"Decision: {'H1' if ell_H0 > ln_eta_NP else 'H0'}\n")

# Compute for Example 3
ell_edge = compute_log_likelihood_ratio(y1_edge, y2_edge, b, sigma, k)
print(f"Example 3: Observations = ({y1_edge}, {y2_edge})")
print(f"Log-Likelihood Ratio (ell) = {ell_edge:.4f}")
print(f"Decision: {'H1' if ell_edge > ln_eta_NP else 'H0'}\n")

Example 1: Observations = (2.0, 3.0)
Log-Likelihood Ratio (ell) = 1.2500
Decision: H1

Example 2: Observations = (-1.0, 0.0)
Log-Likelihood Ratio (ell) = -0.2500
Decision: H0

Example 3: Observations = (1.0, 1.0)
Log-Likelihood Ratio (ell) = 0.5000
Decision: H0

import numpy as np
import matplotlib.pyplot as plt

# ===============================
# 1. Define Parameters
# ===============================

# Signal parameters
b = 0.5          # Signal amplitude
sigma = 2.0      # Noise standard deviation
k = 2            # Number of samples

# Neyman-Pearson Threshold
eta_NP = 1.928
ln_eta_NP = np.log(eta_NP)  # Approximately 0.6564

# Decision boundary calculation:
# ln(eta_NP) = (2b / sigma^2) * (y1 + y2)
# => y2 = (ln(eta_NP) * sigma^2) / (2b) - y1
y2_intercept = (ln_eta_NP * sigma**2) / (2 * b)
# So, y2 = y2_intercept - y1

# ===============================
# 2. Define Decision Boundary
# ===============================

def decision_boundary(y1):
    return y2_intercept - y1

# ===============================
# 3. Define Observations
# ===============================

observations = {
    'Example 1: H1': {'y1': 2.0, 'y2': 3.0, 'decision': 'H1'},
    'Example 2: H0': {'y1': -1.0, 'y2': 0.0, 'decision': 'H0'},
    'Example 3: H0': {'y1': 1.0, 'y2': 1.0, 'decision': 'H0'}
}

# ===============================
# 4. Create Plot
# ===============================

plt.figure(figsize=(10, 8))

# Define range for y1
y1_values = np.linspace(-5, 5, 400)
y2_values = decision_boundary(y1_values)

# Plot decision boundary
plt.figure(figsize=(10, 6))
plt.plot(y1_values, y2_values, 'g--', label='Decision Boundary')

# Fill regions
plt.fill_between(y1_values, y2_values, y2_values + 10, color='red', alpha=0.1, label='Decide $H_1$')
plt.fill_between(y1_values, y2_values, y2_values - 10, color='blue', alpha=0.1, label='Decide $H_0$')

# Plot observations
for label, obs in observations.items():
    y1 = obs['y1']
    y2 = obs['y2']
    decision = obs['decision']
    if decision == 'H1':
        color = 'red'
        marker = 'o'
    else:
        color = 'blue'
        marker = 's'
    plt.scatter(y1, y2, color=color, edgecolor='k', s=100, marker=marker, label=label)

# Prevent duplicate labels in legend
handles, labels = plt.gca().get_legend_handles_labels()
by_label = dict(zip(labels, handles))
plt.legend(by_label.values(), by_label.keys())

# Labels and Title
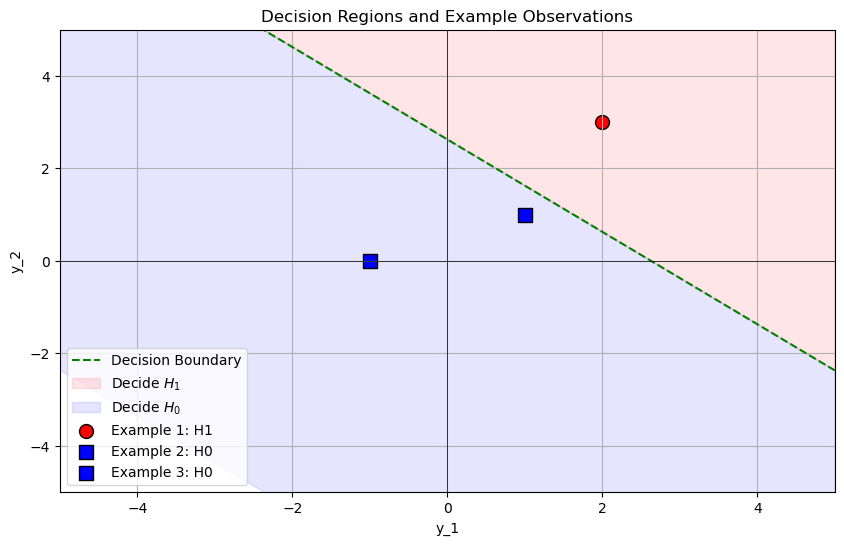
plt.title('Decision Regions and Example Observations')
plt.xlabel('y_1')
plt.ylabel('y_2')
plt.xlim(-5, 5)
plt.ylim(-5, 5)
plt.grid(True)
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.legend(by_label.values(), by_label.keys(), loc='lower left')

plt.show()

<Figure size 1000x800 with 0 Axes>

_images/0cc4acd98341ffb5d59d870d29bd986997a6b9ce77611ae7a895ff533618a02a.png

Example: Antipodal Signal Detection using Multiple Samples

Contents

Example: Antipodal Signal Detection using Multiple Samples#

Step 1: Conditional PDFs Extending to \( k \) Independent Samples#

Step 2: Computing the Likelihood Ratio#

Log-Likelihood Ratio#

Step 3: Make Decision#

Neyman-Pearson (NP) Criterion#

Derivation of the Neyman-Pearson Threshold (\( \eta_{\text{NP}} \))#

Derivation of the Probability of Detection (\( P_d \))#

Numerical Results#

Real-World Application Example#

Example 1: Deciding \( H_1 \) (Signal Present)#

Example 2: Deciding \( H_0 \) (No Signal)#

Example 3: Edge Case Near the Threshold#