Discrete System and Equivalent Discrete Model#
Transitioning from continuous-time to discrete-time models is fundamental in modern communication systems, primarily due to the prevalence of digital processing techniques.
This section elaborates on sampling continuous-time signals \( x(t) \) and \( y(t) \) at a sampling rate of \( W_s \) samples/second.
Sampling Process#
Sampling Rate (\( W_s \)): The number of samples taken per second from the continuous-time signals \( x(t) \) and \( y(t) \).
It must satisfy the Nyquist-Shannon Sampling Theorem to prevent aliasing.
where \( W_{\text{max}} \) is the maximum frequency component present in the signal.
Bandwidth (\( B \)) vs. Sampling Rate (\( W_s \)): To avoid confusion, it’s crucial to distinguish between the signal bandwidth and the sampling rate.
Ensure that the signal bandwidth \( B \) satisfies \( B \leq \frac{W_s}{2} \).
Sampling Continuous-Time Signals#
Given continuous-time signals \( x(t) \) (transmitted signal) and \( y(t) \) (received signal), sampling at rate \( W_s \) yields discrete-time sequences \( x_b[m] \) and \( y_b[m] \), where \( m \) is an integer index representing the sample number.
Reconstruction Theorem:
The continuous-time baseband signal \( x_b(t) \) can be reconstructed from its samples \( x_b[m] \) using the sinc interpolation formula:
where
Sampling Rate (\( W_s \)): Explicitly denoted as \( W_s \), which equals \( 2W_{\max} \).
Sampling Interval: \( T_s = \frac{1}{W_s} = \frac{1}{2W_{\max}} \)
Samples: \( x_b[m] \) represents the sampled values of \( x_b(t) \) at integer multiples of \( T_s \), i.e., \( x_b[m] = x\left(\frac{m}{W_s}\right) = x\left(\frac{m}{2W_{\max}}\right) \)
Sinc Function Argument: \( \text{sinc}\left( W_s t - m \right) = \text{sinc}\left(2W_{\max} t - m \right) \)
Note that
The sinc functions act as ideal low-pass filters that interpolate between samples to reconstruct the original continuous-time signal.
Alternative Expression
Sampling Rate (\( W_s \)): Here, \( 2W_{\max} \) is the Nyquist sampling rate (\( W_s \)), where \( W_{\max} \) is the maximum frequency of the band-limited signal \( x(t) \).
Sampling Interval: \( T_s = \frac{1}{W_s} = \frac{1}{2W_{\max}} \)
Samples: \( x\left(\frac{n}{2W_{\max}}\right) \) represents the sampled values of \( x(t) \) at intervals of \( T_s \).
Sinc Function Argument: \( \text{sinc}\left(2W_{\max} \left(t - \frac{n}{2W_{\max}}\right)\right) = \text{sinc}(2W_{\max} t - n) \)
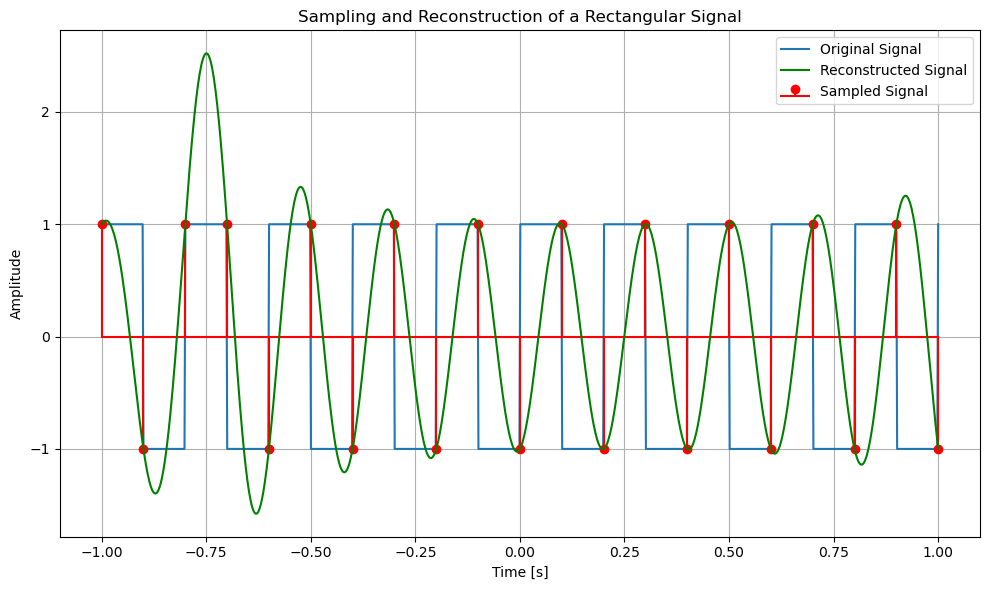
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import square
# Define the frequency of the rectangular signal
f0 = 5 # frequency in Hz
# Define the time vector with a high enough resolution
t = np.linspace(-1, 1, 1000)
# Create the rectangular signal using the square function
rect_signal = square(2 * np.pi * f0 * t)
# Define the Nyquist rate, which is twice the highest frequency
W_max = f0 # highest frequency contained in the signal is f0
fs = 2 * W_max # Nyquist rate (twice the highest frequency)
# Example of undersampling (below the Nyquist rate)
# fs = 0.7 * W # Note: This is below the Nyquist rate and may cause aliasing
# Sample the signal at the Nyquist rate
sample_times = np.arange(-1, 1 + 1/fs, 1/fs)
sampled_signal = square(2 * np.pi * f0 * sample_times)
# Reconstruction using sinc interpolation
T = 1 / fs # sampling interval
reconstructed_signal = np.zeros_like(t)
for n in range(len(sampled_signal)):
# Shifted sinc functions for each sample
reconstructed_signal += sampled_signal[n] * np.sinc((t - sample_times[n]) / T)
# Plotting the original and sampled signals along with the reconstructed signal
plt.figure(figsize=(10, 6))
# Original signal
plt.plot(t, rect_signal, linewidth=1.5, label='Original Signal')
# Sampled signal
plt.stem(sample_times, sampled_signal, linefmt='r-', markerfmt='ro', basefmt='r-', label='Sampled Signal')
# Reconstructed signal
plt.plot(t, reconstructed_signal, linewidth=1.5, color='g', label='Reconstructed Signal')
# Labels and title
plt.xlabel('Time [s]')
plt.ylabel('Amplitude')
plt.title('Sampling and Reconstruction of a Rectangular Signal')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
Equivalent Discrete-Time Model#
The equivalent discrete-time baseband model of the discrete passband communication system is expressed as:
where:
\( y_b[m] \): Received discrete-time signal.
\( h_b[m] \): Discrete-time channel impulse response.
\( x_b[m] \): Transmitted discrete-time signal.
\( n_b[m] \): Discrete-time additive noise.
Convolution (\( \ast \)): Represents the discrete convolution operation between \( h_b[m] \) and \( x_b[m] \).
Discrete Channel Impulse Response \( h_b[m] \)#
The discrete-time channel impulse response \( h_b[m] \) is derived from the continuous-time baseband channel \( h_b(t) \) as follows:
Explanation:
Projection onto Sinc Function: This integral projects the continuous-time channel \( h_b(t) \) onto the discrete-time domain by convolving it with the sinc function and sampling at \( t = \frac{m}{W_s} \).
Ideal Low-Pass Filter Assumption: The sinc function acts as an ideal low-pass filter that preserves the baseband characteristics during sampling.
Discrete Received Signal \( y_b[m] \)#
The discrete-time received signal \( y_b[m] \) is obtained by sampling the baseband received signal \( y_b(t) \) at \( t = \frac{m}{W_s} \):
Explanation:
Baseband Received Signal: \( y_b(t) = h_b(t) \ast x_b(t) + n_b(t) \), where \( n_b(t) \) is the baseband noise.
Sampling: Sampling \( y_b(t) \) at discrete intervals \( \frac{m}{W_s} \) yields \( y_b[m] \).
Discrete-Time Noise Model \( n_b[m] \)#
The discrete-time noise \( n_b[m] \) is derived from the continuous-time baseband noise \( n_b(t) \):
Autocorrelation Function \( R_{n_b}[l] \):
It should be clarified that \( R_{n_b}[l] \) is derived from the continuous autocorrelation function \( R_{n_b}(t) \) evaluated at \( t = \frac{l}{W_s} \).
Explanation:
Discrete Autocorrelation: \( R_{n_b}[l] \) represents the autocorrelation of the discrete noise \( n_b[m] \) at lag \( l \).
Continuous-to-Discrete Mapping: The autocorrelation at discrete lag \( l \) corresponds to the continuous autocorrelation at \( \frac{l}{W_s} \).
Stationarity Assumption: It is assumed that the noise \( n_b[m] \) is Wide-Sense Stationary (WSS), meaning \( R_{n_b}[l] \) depends only on the lag \( l \), not on the absolute time index \( m \).
Summary of Discrete Model#
The complete discrete-time model is as follows:
Discrete-Time Received Signal:
\[ y_b[m] = h_b[m] \ast x_b[m] + n_b[m] \]Reconstruction of Baseband Transmitted Signal:
\[ x_b(t) = \sum_{m=-\infty}^{\infty} x_b[m] \cdot \text{sinc}\left( Wt - m \right) \]Sampling of Baseband Received Signal:
\[ y_b[m] = y_b\left( \frac{m}{W_s} \right) \]Discrete-Time Channel Impulse Response:
\[ h_b[m] = \int_{-\infty}^{\infty} h_b(\tau) \cdot \text{sinc}\left( W\left( \tau - \frac{m}{W_s} \right) \right) d\tau \]Discrete-Time Noise Autocorrelation:
\[ \boxed{ R_{n_b}[l] = R_{n_b}\left( \frac{l}{W_s} \right) } \]
